均值－方差资产组合分析

---

由马科维茨(Markowitz，1959)发展的一种特殊而有重要应用的资产组合选择方法。

它假设投资者的效用由资产组合P的回报均值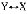_p和回报的方差σ#决定，即效用函数形如v(#_p，σ#)，且v₁＞0和v₂＜0，此处下标表示对第一、二个变量求偏导数。这意味著投资者认为#_p越大越好，σ#越小越好。

考虑n种资产，记资产i的回报为#_i，i=1，2，…，n。投资者把全部资金分别投入到这n种资产上，设投到资产i上的资金占总资金的份额为w_i，则#w_i=1。

称向量(w₁，…，w_n)为一个资产组合。此资产组合的回报为#_p=#w_i#_i，从而组合的期望回报和方差分别为#_p=#w_i#_i和σ#=#w_iw_jσ_ij，其中σ_ij是#_i和#_j的协方差。

在上述假设的效用函数下，备选的最优资产组合必定具有性质：对一个给定的方差水平，它有最大的期望回报，同时，对一个给定的期望回报水平，它有最小的方差，具有这种性质的资产组合称为均值－方差有效的。如果仅要求对一个给定的期望回报水平，有最小方差，则称它为最小方差资产组合。

从数学上求最小方差资产组合可写成解：

min σ#，s．t．R_p=K

求有效均值－方差组合可写成解

max R_p，s．t．σ#=L

令K和L连续变化，就求得最小方差资产组合的集合和有效均值一方差资产组合的集合。

可以证明，最小方差资产组合的集合是σ_p－#_p坐标平面上的一条双曲线的一支，有效均值－方差资产组合的集合则是这一支的上半支。投资者按自己的偏好在这上半支选择投资组合。