均值非线性

---

如果一时间序列的随机误差ε_i的条件均值与前几次观测的误差项之间的关系呈非线性，则称该时间序列存在均值非线性。

假设一个时间序列X_t可以表示为：

X_t=f(ε_t，ε_t1，ε_t－2，…)

其中随机误差项ε_t，ε_t－1，ε_t－2，…具有零均值和单位方差，f(·)是某个未知函数。经研究发现X_t总可以表示成下式：

X_t=g(ε_t－1，ε_t－2，…)+ε_th(ε_t－1，ε_t－2，…)

其中g(·)表示X_t以过去信息为条件的条件均值，即E_t－1[X_t]=g(ε_t－1，ε_t－2，…)；X_t随ε_t成比例的变动，h(·)表示比例系数。h(·)的平方就是X_t以过去信息为条件的条件方差。

即

E_t－1[X_t－E_t－1[X_t]]²=h²(ε_t－1，ε_t－2，…)

带有非线性函数g(·)的模型就称为均值非线性。

下面是一个简单的均值非线性的例子：

X_t=ε_t+αε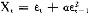_－1

在该模型中g(·)=αε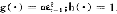_－1；h(·)=1。