反馈控制系统的特性设计

---

5．3．1 概述

系统控制特性设计的实质，就是系统数学模型的设计，即设计能满足给定性能(稳定性、响应快速性、稳态精度)指标要求，且在物理上可实现的数学模型。

被设计的系统，一般可分为两部分，一部分由执行元件和被控对象等构成。在系统设计时，根据要求选定这部分的元件或部件后，其数学模型就是固定的，因此称这部分是系统的不可变部分。另一部分由放大器等参数可调的元件构成，这部分称为系统中的可变部分。如果对系统性能要求不高，有时通过对可变部分参数的调节，如改变放大器增益，就可以满足要求。但在多数情况下，单由调节这些参数是无法使系统同时满足各项性能指标要求的。例如，提高放大器增益即增大开环增益，虽然可减小系统的稳态误差，但可能引起系统不稳定。因此，在系统设计中，常引入辅助装置来改善系统的性能。这种对系统性能的改善，称为对系统的校止(或补偿)，系统中引入的辅助装置称为校正装置(或补偿装置)。

由上述可知，当系统中不可变部分的元、部件选定后，则系统数学模型中就有一部分已经确定了。因此，为使系统满足给定性能指标的特性设计，就是确定系统可变部分和校正装置的数学模型。在经典控制理论中，确定校正装置数学模型常用的方法是频率响应法。由于对数坐标图绘制简单、方便，所以工程上多采用对数坐标图设计串联校正装置的数学模型。

对数频率特性曲线的形状，可以表征系统的性能。对于最小相位系统，对数幅频特性和对数相频特性一一对应，见图1．9－40，因此，研究最小相位系统性能时，只要研究对数幅频特性曲线即可。

在开环对数幅频特性曲线的低频段，可以了解开环传递函数中所含积分环节的个数v和开环增益K的数值。因此，曲线低频段的形状表征了闭环系统的稳态性能；在开环对数幅频特性曲线的中频段，可以了解幅值穿越频率ω_。的大小和对数幅频特性穿越零分贝线时的斜率(该斜率决定著系统的稳定性，由图1．9－40可以推知，若对数幅频特性以－20dB／dec斜率穿越零分贝线，且该斜率占有一定的频带宽度，系统肯定是稳定的)。而开环对数幅频特性曲线中频段的形状表征了系统的响应快速性和稳定性，其高频段的形状表征了系统的复杂性和滤波性能。

用频率法对系统进行校正，就是在系统中加入频率特性形状合适的校正装置，使系统开环频率特性曲线变成所希望的形状，即低频段增益充分大，以保证稳态误差要求；中频段的斜率应等于一20dB／dec，并占据充分宽的频带，以保证系统具有足够的相角裕量；高频段幅值应尽快衰减，以使噪声影响减到最小程度。由于一般系统高频段的形状都能满足要求，所以对系统进行校正时，可保持高频段形状不变。

5．3．2 校正网络的设计

工程中常用的校正方式有：串联校正和并联校正，校正装置串联在系统的前向通路中称为串联校正，如图1．9－41所示。图中，G_e(s)为校正装置的传递函数。为了减小功率损耗，串联校正装置一般都放在前向通道的前端，即低功率部分。串联校正按校正环节的性质又可分为相位超前校正、相位滞后校正和相位滞后一超前校正。并联校正按校正环节G_e(s)的并联方式可分为反馈校正，如图1．9－42所示；顺馈校正，如图1．9－43所示。

(1)串联相位超前校正

图1．9－44所示为RC超前网络。若输入信号源的内阻为零，输出端负载阻抗为无穷大，则网络的传递函数为

例1．9－18 已知单位反馈控制系统的开环传递函数为

❸ 确定超前网络应提供的最大超前相角φ_m。仅从要求的相角裕量和未校正系统现有相角裕量来看，需要的最大超前相角为γ_e2－γ_c1=45°－12°45′=32°15′。但实际应由超前网络提供的最大超前相角应大于该值。因为系统加入超前校正网络后，幅值穿越频率会右移，即补偿后新的幅值穿越频率ω_c2大于补偿前的幅值穿越频率ω_o1，其差值为arg〔G(jω_c1)－G(jω_c1)〕，因此，由超前网络提供的最大超前相角应是：

φc=γ_c2－γ_c2+arg〔G(jω_e1)－G(jω_c2)〕一般取arg〔G(jω_c1)－G(jω_c2)〕==3°～5°，此处取为3°45′，则可得

φ_m=32°15′+3°45′=36°

❹ 确定超前正装置的传递函数：

由式 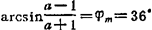可求出衰减系数a=3．85。

为了充分利用超前网络的最大超前相角，选ω_m和校正后的幅值穿越频率ω_c2相等，以确定ω_c2。由此可得关系式

201g|G(jω₂)|+10lga=0

201g|G(jω_c2)|=－10lga=－10lg3．85

=－5．9(dB)

由图1．9－46校正前曲线可查出幅值为－5．9dB时的频率为6．2s^－1，即：ω_c2=ω_m=6．2s^－1。

根据式(1．9－62)可求出超前网络的参数T为

采用滞后网络对系统进行校正，不是利用其相角滞后特性，而是利用其高频幅值衰减特性使原系统获得足够大的相角裕量，以提高系统的相对稳定性．当系统的动态性能满足要求时，也可利用滞后网络改善系统的稳态性能。利用滞后网络校正系统时，b值不宜取得过小，一般取0．1左右。

例1．9－19 已知单位反馈控制系统的开环传递函数为

上例表明，对于选定的开环增益K，采用滞后校正后，其幅值穿越频率减小，相角裕量变大，从而提高了系统的稳定程度和抑制高频噪声的能力，但降低了系统的响应快速性。采用串联相位滞后校正，既能够提高系统的稳态精度，而又基本上不改变系统的动态性能。以图1．9－49为例，如果将已校正系统对数幅频特性曲线向上平移18dB，则校正前后的相角裕量和幅值穿越频率基本不变，即动态性能基本不变，而系统开环增益却提高7．94倍，即提高了系统的稳态精度。由此可知，若未校正系统动态性能已满足要求，而稳态性能不满足要求时，可利用串联相位滞后校正提高系统的稳态精度，而保持其动态性能基本不变。

(3)串联滞后——超前校正

滞后——超前校正具有响应速度快、超调量小和抑制高频噪声性能好等优点。当未校正系统不稳定，而且对相角裕量、响应速度及稳态精度要求都较高时，可采用滞后——超前校正。

串联滞后——超前校正可用图1．9－47所示的RC滞后网络经隔离放大器，再串接图1．9－44所示的RC超前网络构成。但为了减少元件，通常采用如图1．9－50所示具有滞后——超前相位特性的网络。该网络的传递函数为

设式(1．9－65)分母有两个不相等的负实根，则式(1．9－65)可写成

利用滞后——超前网络对系统进行校正，一般有固定的步骤。通常是将设计相位滞后装置和设计相位超前装置两种方法结合起来，并用逐步试探法找出比较满意的设计方案。

例1．9－20 已知单位反馈控制系统的开环传递函数为

❸ 确定滞后——超前校正装置的传递函数：

试选未校正系统相位滞后为－180°时的频率ω=1．5为校正后系统的幅值穿越频率ω_c2，则校正后在频率处的相位裕量应有50°。选择滞后部分的较高的转折频率ω₂=ω_c2／10=1．5／10=0．15；取β=10，则滞后部分的较低的转折频率为ω₂／β=0．015。于是可得滞后部分的传递函数为

(5)反馈校正

反馈校正的基本原理是，用反馈校正装置包围未校正系统中对动态性能有重大影响的环节，形成局部反馈回路，以改善系统的性能。图1．9－42所示反馈校正系统的开环传递函数为

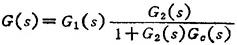
当|G₂(s)G_c(s)|》1时，局部反馈部分的等效传递函数为

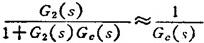
即反馈校正后系统的特性几乎与被反馈校正装置包围的环节无关。而当|G₂(s)G_c(s)|《1时，G(s)≈G₁(s)G₂(s)，即此时已校正系统与未校正系统特性一致。因此，适当选取反馈校正装置G_e(s)的参数，可以使已校正系统特性发生期望的变化。在工程中进行系统设计时往往把|G₂(s)G_c(s)|》1的条件简化为|G₂(s)G_c(s)|＞1。简化的结果，虽然会产生一定的误差，但该误差属于工程允许误差范围之内。

反馈校正的特点是：被局部反馈所包围部分的元件的非线性或参数的波动对控制系统性能的影响可以忽略；反馈校正(一般指负反馈校正)有减小被包围环节时间常数的能力，从而有助于加快整个系统的响应速度，此外，进行反馈校正时，应注意局部反馈回路的稳定。如果反馈校正装置参数选择不当，而使系统局部反馈回路失去稳定，则整个系统也难以稳定可靠地工作，且不便于对系统进行调试。