反比例函数

---

一般地，如果两个变量x，y之间的关系可以表示成y=k/x(k≠0)形式，那么称y是x的反比例函数．

注意 1．反比例函数的自变量x不能为零．

2．反比例函数解析式中只有一个基本量k(k≠0)故只需一个条件，就可以确定其表达式．

3．当常数k≠0时，xy=k与y=k/x两种表达式形式是等价的，但前者是隐函数形式，作为反比例函数，应表示成显函数形式．

例1 下列函数中，哪些是反比例函数?

(1)面积不变时，三角形的底和高；

(2)正方形的面积和边长；

(3)圆的周长和半径；

(4)做匀速运动的物体，走完固定路程所需时间与运动速度；

(5)除数不变时，被除数与商；

(6)某人的年龄与体重．

答 (1)(4)．

[解析] (1)因为三角形面积S为常量，所以底a和高h满足关系式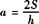，即底是高的反比例函数．

(2)正方形的面积S和边长a的关系式是S=a²，因此S不是a的反比例函数．

(3)圆的周长C和半径r满足C=2πr，因此圆的周长C不是半径r的反比例函数，而是正比例函数．

(4)路程s为常量，时间t与速度v的关系式t=s/v，因此时间t是速度v的反比例函数．

(5)除数b为常量，被除数a与商c的关系式为a=bc，因此被除数a不是商c的反比例函数，而是正比例函数．

(6)某人的年龄与体重没有固定的关系，不成反比例．

例2 已知函数y=(n²+2n)x^n2+n－1(n为常数)，问当n为什么数时函数y=(n²+2n)x^n2+n－1是反比例函数?

解 由反比例函数定义，得

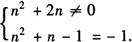
解得，n=－1，此时函数y=(n²+2n)x^n2+n－1的解析式为：y=－1/x．

[解析] 反比例函数y=k/x还可以写成y=kx^－1的形式，即x的幂指数为－1．

例3 已知x与y成正比例，y与1/z成正比例，则x与z之间成( )．

A．正比例

B．反比例

C．正比例或反比例

D．以上都不对

答 B．

[解析] ∵x与y成正比例，

∴x=k₁y(k≠0)．

又∵y与1/z成正比例，

∴y=k₂·1/z(k₂≠0)．

∴x=k₁k₂·1/z(k₁k₂≠0)．

∴x与z之间成反比例．