随机过程

概率论的基本内容之一。随参数变化的随机变量簇，通常取时间作为参数。例如由大量元件组成的一个设备，出故障的元件立即被替换，从时刻t₀到t的时间间隔内要替换的元件数就是随时间变化的随机变量簇。最主要的有马尔可夫过程、平稳过程、可加过程、分枝过程等。在可靠性理论中应用较多。

随机过程Stochastic Process

概率论和数理统计研究主要的是一个或有限个随机变量。在极限定理中，虽然涉及了无穷多个随机变量，但它们之间经常是相互独立的。在随机过程中，将要研究一族无穷多个、相互有关的随机变量，记为{X(t),t∈T}，其中，T是一个无穷集合。最常见的有：(1) T₁＝{0,1,2,3，…},(2)T₂＝{…，-3,-2,-1,0,1,2,3，…},(3)T₃＝[a,b]，其中a,b可以是±∞。由于t一般表示时间，通常就称它们为随机过程。随机过程就是一族无穷多个随机变量{X(t),t∈T}，也可称它为随机函数，其中的T又称为参数集。当T为(1),(2)两种情形时，也称为随机序列。随机过程的理论产生于20世纪初，是由于物理学、通讯与控制，管理科学等方面的需要而逐步发展起来的，它的研究领域包括马尔可夫过程、二阶矩过程等。

随机过程Stochastic Process

一连串随机事件动态关系的定量描述。随机过程理论产生于20世纪初，它是由于物理学、生物学、通信与控制、管理科学等方面的需要而逐步发展起来的。例如，某电话站在某一时间段内接到的用户的呼叫次数就是依赖时间t的一组随机变量。常见且重要的随机过程有马尔科夫过程和平稳随机过程。

随机过程

随时间变化而变化的随机变量的集合。

随机过程

亦称 “随机函数”。描述对随机现象进行不断地观测所得结果的数学模型。用 {Xt (ω),t∈T} 表示一族无穷多个、相互关联的随机变量，其中T是一个参数集，为无穷集合。常见的有❶T1 =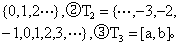通常t指时间，根据t的取值是否连续，随机过程可以分为连续型和离散型两种。随机过程是参数t和样本空间上点ω的函数。对随机过程Xt (ω) 进行观察，就得到一个Xt (ω) 的 “实现”。在为离散的情况下，就形成一个序列，即 “时间序列”。

随机过程stochastic process

亦称“随机函数”。描述对随机现象进行不断地观测所得结果的数学模型。用{Xt(ω),t∈T}表示一族无穷多个、相互关联的随机变量，其中T是一个参数集，为无穷集合。常见的有❶T₁＝{0,1,2…},
❷T₂＝{…，-3,-2,-1,0,1,2,3，…},
❸T₃＝[a,b]。通常t指时间，根据t的取值是否连续，随机过程可以分为连续型和离散型两种。随机过程是参数t和样本空间上点ω的函数。对随机过程Xt(ω)进行观察，就得到一个Xt(ω)的“实现”。在为t离散的情况下，就形成一个序列，即“时间序列”。

随机过程

依赖于参数的一族随机变量的全体。参数通常是时间。随机变量是随机现象的数量表现，其取值随着偶然因素的影响而改变。例如，某商店在从时间t₀到时间tK这段时间内接待顾客的人数，就是依赖于时间t的一族随机变量，即随机过程。随机过程的理论产生于本世纪初期，是应物理学、生物学、管理科学等方面的需要而逐步发展起来的。目前，在自动控制、公用事业、管理科学等方面都有广泛的应用。