分析法设计平面连杆机构

---

采用分析法设计平面连杆机构，需先建立机构参数与运动条件之间的关系式，然后根据关系式采用不同的数学方法(如向量、复数、矩阵、旋量等)，按一定的准则，求解满足给定运动条件的机构未知参数。这里将介绍位移矩阵设计法和复数封闭环设计法。

3．2．1 刚体导引机构的设计

1．位移矩阵设计法

如图5．4-19所示，当平而刚体S由位置S₁运动到位置S_j，若已知基点P的位置坐标(p_jx、P_jy)及标线PQ的对应位置角θ_j，则根据线性代数待求点Q的位置可表示为：

四、五个位置设计：给定连杆四个位置，设计R-R导引杆时，式(5．4-8)和(5．4-9)中的j=2，3、4，于是可得方程组：

2．复数封闭环设计法

图5．4-24所示为一平面铰链四杆机构在位置1(实线)和任一位置j(虚线，j=2，3，……)的两个不同位置。图中各杆均以向量表示，整个四杆机构可以看作是两个双向量(即标准形)组成Z₁-Z₂和Z₃－Z₄。其中Z₂和Z₄同属连杆平面。在设计中，这四个向量确定了，圆点A、B和圆心点O_A、O_B即随之确定。另两向量Z₅和Z₆也可由下式求得

Z₅=Z₂－Z₄ (5．4-20)

Z₆=Z₁+Z₅－Z₃ (5．4-21)

对于双向量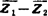来说，其位置1和任一位置j均构成闭环O_AA_jP_jOP₁AO_A，可写出闭环复数方程

Z_1e^iφ_j+Z₂^eia_jR－_j+R₁-Z₂-Z₁=0

(5．4-22)

或Z₁(e^iφ_j－1)+Z₂(^eia_j－1)=δ_j (5．4-23)

式中，δj表示连杆平面上点P从P₁(位置1)到P_j(位置j)的位移向量。若P₁和P_j的位置分别以向量R₁和R_j表示，则

δj=R_j－R₁

式中，φ_j和a_j分别表示向量Z₁和Z₂从位置1到位置j的转角。

式(5．4-23)称为标准形方程，是一复数方程(或向量方程)，分离实部和虚部，可得两个实数方程，能解两个未知实数。另一组双向量Z₃-Z₄，也可得到类似的标准形方程。

由图5．4-24可知，当给定连杆平面一点(例如P)的位置及其方位角时，则该平面的位置即完全确定。位置设计中给定位置的最大可能数见表5．4-9．表中列有给定位置数、实数方程数、未知实量数、任选实量数和解的可能数之间的关系。

表5．4-9 位置设计给定位置的最大可能数

这是给定运动平面三位置的位置设计，其设计方法和步骤如下：

求四杆机构左侧双向量Z₁－2₂(参见图5．4-24)：设φ₂=90°，φ₂=198°，由式(5．4-27)和(5．4-28)得

3．2．2 传动机构的设计

1．位移矩阵设计法

传动机构的设计即是实现给定函数机构的设计，它按两连架杆给定的若干组对应位置确定机构的设计参数。对该类型机构的设计，通常是转化为实现刚体导引机构的设计。

实现给定函数的传动机构，由于两连架杆的位置关系仅与各杆的相对长度有关，故进行设计时一般选取机架的长度A₀B₀=1。图5．4-29所示铰链四杆机构，即取固定铰链中心A0为坐标原点，另一固定铰链中心B0的坐标为(1，0)。若将机构的第j个位置B_jB₀A₀A_j看成一刚体，并绕B_o点转过(－ψ_1j)=－(ψ_j－ψ₁)，使从动连架杆B₀B_j与B_oB₁重合，则机构将由位置B_jB₀A₀A_j转到新的位置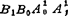，即原从动连架杆转化为“机架”，原机架和连杆转化为“连架杆”，而原主动连架杆转化为“连杆”。于是，通过转换机架法，就把按给定位置φ_j、ψ_j(j=1，2，……，n)设计实现函数机构的问题，转化为按给定的“连杆n的位置A₀A₁、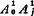(j=1，2，……，n)设计刚体导引机构的问题。因此，利用式(5．4-6)可写出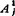的位置方程式

例5．4-6 在上例再增加一精确点x₁=1，y₁=0，试设计近似实现给定函数y=1ogx(1≤x≤2)的铰链四杆机构。^〔21〕

四个精确点为：

x₁=1 y₁=0

x₂=1．067 y₂=0．0282

x₃=1．50 y₂=0．1761

x₄=1．933 y₄=0．2862

对应的转角为：

φ₁=φ₀+0° ψ₁=ψ₀+0°

φ₂=φ₀+4．02° ψ₂=ψ₀+8．43°

φ₃=φ₀+30° ψ₃=ψ_o+52．65°

φ₄=φ_o+55．98° ψ₄=ψ_o+85．57°

相对于第一个位置的转角为：

φ₁₂=4．02° ψ₁₂=8．43

φ₁₃=30° ψ₁₃=52．65°

φ₁₄=55．98° ψ₁₄=85．57°

利用牛顿-莱夫森法解非线性方程组的计算机程序进行迭代求解，当预先选定未知量b12=1．35。并不断给b1x以增量0．2时，可得一系列解如下：

(5．4-54)

据此分析给定对应位置的最大可能数与表5．4-9相同，即为五。这样，实现给定函数的传动机构设计问题的解法，就和导引机构的设计完全一致了。其唯一的区别是，这里的已知量是δ_j和φ_j，而导引机构的设计则是δ_j和a_j。

值得注意的是，实现给定函数的传动设计只需一个双向量，即图5．4-33中的Z₁－Z₅。因此，在给定五组连架杆对应位置时，同五位置设计一样，可得4个、2个或零个双向量组，最多也只能得到4个、2个或零个四杆机构。但其中总有一个解没有实际意义，即|Z₁|=0、Z₅=Z₃，因而a_j=ψ_j。可见，五精确点的设计，最多只能得到三个不同的四杆机构。

3．2．3 导向机构的设计

1．位移矩阵设计法

图5．4-34所示为铰链四杆机构A₀A₁B₁B₀。设连杆AB上一点P在坐标系xoy中，沿平面轨迹的一系列给定的有序点P₁、Pj(j=2、3、4……)运动。由于P_j点的坐标(P_jx、p_jy)为已知，故需确定四个铰链中心A₀、A₁、B₀、B₁的坐标。为此，可列出两连架杆的约束方程：

2．复数封闭环设计法

按图5．4-24所示，四杆机构左右两侧双向量的标准形方程为

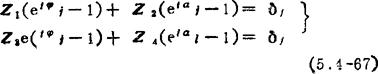
在轨迹设计中，仅已知连杆上P点的位置，即式(5．4-67)中δ_j是唯一的已知量，其余均为未知量。由于式中Z₂和Z₄同属连杆平面，其转角aj相同，因此由一式求得a_j后，将其代入另一式中即为已知量。为此，轨迹设计时应将两侧的标准形方程结合在一起予以讨论。

仿效导引机构设计的分析方法，按式(5．4-67)分析实现轨迹的导向机构设计给定精确点位的最大可能数见表5．4-12。由表可知，给定轨迹精确点位的最大可能数为9。当进行9个精确点的轨迹设计时，需联立求解32个超越方程式。然而，连架杆的转角φj和ψj在设计中并非必求不可。如果将其舍弃，则未知实量数可减少一半，联立方程的总数减为16个，可用开环法按二连架杆长不变建立约束方程。即使如此，求解仍然相当困难。因此，通常是减少给定的精确点位数，任选某些未知量，以简化联立方程组的求解。

表5．4-12 轨迹设计给定精确点位的最大可能数

另一种方法，是按同时给定轨迹上的精确点位P_j和相应的输入杆转角φ_j进行设计。仿前分析式(5．4-67)可知，此时给定精确点位的最大可能数与位置设计相同(也是五个)，方程组的解法也基本一致。这时，就已知量和未知量而言，双向量Z₁-Z₂的标准形方程与函数设计的方程相同，而双向量Z₃－Z₄的标准形方程则与位置设计的一样，两者的解法在本质上无差异，只是后者需待前者求得a_j之后再求。