函数的和、差、积、商的导数

---

1．和(或差)的导数

法则1 两个函数的和(或差)的导数等于这两个函数的导数的和(或差)，即(u±v)′=u′±v′．

2．积的导数

法则2 两个函数的积的导数等于第一个函数的导数乘以第二个函数，加上第一个函数乘以第二个函数的导数，即(uv)′=u′v+v′u．

3．商的导数

法则3 两个函数的商的导数，等于分子的导数与分母的积，减去分母的导数与分子的积，再除以分母的平方，即 ．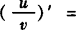

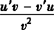例1 求下列函数的导数，并指出其不可导的点．

(1)y=tanx；(2)y=cotx；

(3)y=secx；(4)y=cscx．

4．

(1)求曲线C上横坐标为1的点的切线方程；

(2)第(1)小题中切线与曲线C是否还有其他公共点?

解 (1)把x=1代入C的方程，求得y=—4．

∴切点为(1，—4)．

∵y′=12x³—6x²—18x，

∴切线斜率为k=12—6—18=—12．

∴切线方程为y+4=—12(x—1)，即y=—12x+8．

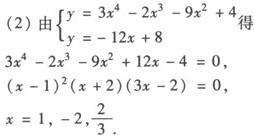
代入y=3x⁴—2x³—9x²+4，求得y=—4，32，0，即公共点为(1，—4)(切点)，(—2，32)，(2/3，0)．

除切点外，还有两个交点(—2，32)，(2/3，0)．

此例告诉我们：曲线与直线相切，并不一定只有一个公共点，当曲线是二次曲线时，我们知道直线与曲线相切，有且只有一个公共点，这种观点对一般曲线不一定正确．

例3 求和1+2x+3x²+…+nx^n—1(x≠1)．

解 由求导公式(xⁿ)′=nx^n—1，可联想到它是第一个和式x+x²+x³+…+xⁿ的导数．

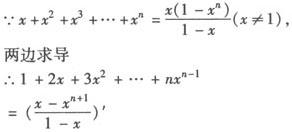
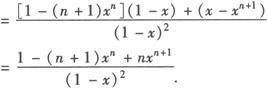
利用本题的结论和方法我们还可以求2+6x+12x³+…+n(n—1)x^n—2的和，请读者自己完成．