共点、共线、共面问题

---

1．证线共点证线共点，基本途径是先确定两直线的交点，其次再证其他直线也经过这个点，一般说来，共点的这些直线常常是平面的交线．

2．证点共线 证点共线，基本途径是先证这些点均落在两个相交平面内，再依照公理2，它们必落在其交线上．

3．证点(线)共面 证点(线)共面，基本途径有两条：其一是先由某些元素确定一个平面，再证其余元素都在这一平面内：其二是先证这些元素分别在两个或多个平面内，再证这些平面重合．

例1 如图，已知△ABC在平面α外，直线AB、AC、BC分别与α交于E、F、G，求证：E、F、G三点共线．

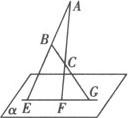
策略 要证明E、F、G三点共线，只需证明点G在AB与AC确定的平面β与α的交线上．

证明 设经过AB、AC的平面为β．

∵AB、AC分别与平面α相交于E、F两点，

∴β∩α=直线EF．

又∵BC∩α=G，且直线，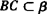

∴G∈直线EF=β∩α，即E、F、G三点共线．

点评 证明三点共线，一般先证两点确定的直线是某两个平面的交线，再证第三个点是两平面的一个公共点，证明“点在直线”．“三点共线”、“三线共点”的命题，通常用公理2．

例2 三个平面α、β、γ两两相交于三条直线，即α∩β=c，β∩γ=a，γ∩α=b，已知直线a和b不平行．

求证：a、b、c三条直线必过同一点．

策略 证若干直线共点时，应先找出其中两条直线的交点，再找出其余直线所在的平面，证明交点是已知直线所在两个平面的公共点．

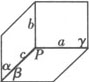
证明 ∵α∩γ=b，β∩γ=a

∴．

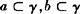∵a、b不平行，

∴a、b必相交，设a∩b=P．

∵P∈a，，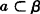

∴P∈β，同理P∈α．

而α∩β=c，∴P∈c．

∴a、b、c相交于一点P．

即a、b、c三条直线过同一点．