债券价格的计算

---

(一)债券价格

投资者根据期望的收益率确定债券的购买价格。为简单起见，先作如下假设：

(1)债券发行者在规定日期肯定偿还债务，暂不考虑债券发行者不能按期还债的可能。

(2)债券有固定的到期日，暂不考虑无固定到期日的债券。

(3)债券价格是指某票息支付日刚刚支付票息后的价格，暂不考虑相邻两个票息支付日之间某个日期的债券价格。

(4)暂不考虑纳税。

(5)涉及的利率均为复利。

再约定一些计算债券价格所用的符号：

P：债券的价格(price)。

F：债券的面值(par value或face account)，印在债券上，它的惟一目的是确定债务人的一系列的偿付额。

C：债券的赎回值(redemption value)，即在债券赎回日支付给债券持有人的货币额。由于债券一般在到期日以面值赎回，因而C往往等于F。以后除特别指出外均假设债券以面值赎回。

r：债券的票息率(coupon rate)，即用于每个票息支付周期(period简称期)计算票息额的比率。票息支付频率，如半年一次或者一年一次。

Fr：票息额，投资者按期收到的债券利息额。

g：债券的修正票息率(modified coupon rate)，是单位赎回值中的票息额，g=Fr／C。g与r的计息频率总是相同的。债券以面值赎回时，g=r。

i：债券的收益率(yield rate)，常称为到期收益(yield to maturity)，是投资者购入债券直至赎回或到期后实际挣得的利率，在“长期债券投资的核算”一节中称为实际利率。以后除非特别指出外，都认为i与r的计息频率相同，并假设i是常数。

n：从债券计算日至债券到期日或赎回日期间的票息支付周期数。

K：到期日或赎回日的赎回值以收益率计算的现值，K=Cvⁿ以i计算。

G：债券的基本额(base amount)，G=Fr／i。

在发行债券的条款中，F、C、r、g、t都是已知的，债券到期前这些参量都不变，它们决定了债务人未来的付出额。而P和i在债券到期前都可以变化，它们成反比关系。债券收益率随金融市场上同类债券主导利率(prevailing rates of interest)上下波动。因而，波动的市场利率将导致债券价格的波动。

债券价格等于各期票息现值加债券赎回值的现值．

半年票息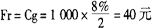

第一期利得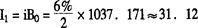

第一期本调P₁=Cg－I₁=40－31．12=8．88

第一期末账面值B₁=B₀－P₁=1037．17－8．88=1028．29

表3－2－4 面值1000元、2年期、息票率8%半年复利、收益率6%半年复利的债券的分期偿债表

债券公平价、应计票息、市价的计算有三种方法。第一种叫理论法(theoretical method)，用复利来准确计算。显然，

故市价或面值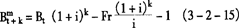

第二种叫实践法(practica method)，对片段时间k用单利来近似计算。那么公平价

用线性插值法也可得此公平价。因该票息期期初公平价为Bt、期末支付票息前的公平价为

B_t+1+Fr，所以有

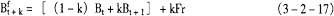
可以证明(3－2－17)式与(3－2－16)式等价。

实践法计算的应计票息为

Fr_k=kFr (3－2－18)

故

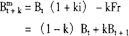
第三种叫半理论法(semi-theoretical method)，综合以上两种方法，用理论法计算公平价，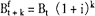

用实践法计算票息

Fr_k=kFr

故

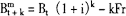
半理论法有一个明显的偏差。对于i=g、P=C的债券，不存在溢价或折价摊销，在所有票息支付日的账面值都相等，因而所有的周期内账面值也等于票息支付日的账面值(即图3－2－3中的虚线平行于横轴)。理论法和实践法都符合此特性只有半理论法例外。但在实践中，半理论法用得最多。期限在6个月以上的债券都用半理论法计算。三种算法中，k的取值根据精确／精确法或30／360法计算而得。

图3－2－3是根据实践法算出的值画出的，公平价与市价在每个票息期都是线性的。票息支付期间购买的债券，属于溢价购买还是折价购买，判断的依据是市价或账面值而不是公平价。例如，面值1000元的债券，市价为980元，另有应计票息30元。虽以1010元的价格购买，但仍是折价购买，因为市价小于赎回值。所以有，

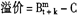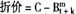，当i＜g

，当i＞g

例：对表3－2－4所述债券，购买5个月后，分别用三种方法计算其公平价、应计票息和市价(账面值)。

解：k=5／6，B₀=1037．17，i=6%÷2=3%，1+i=1．03，Fr=40

理论法：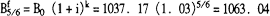

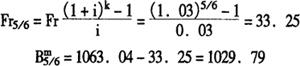
实践法：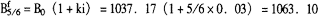

Fr_5／6=kFr=5／6×40=33．33

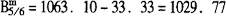
半理论法：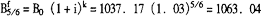

Fr_5／6=kFr=5／6×40=33．33=01063．04－33．33=1029．71