线性回归linear regression

建立不同变量相互关系的线性数学模型数量关系式的统计方法。一变量的取值确定后，另一变量的取值也被确定称为确定性关系。农业化学中一变量取值受其他变量的影响，而存在着对应的统计学规律性，称为相关关系。引起数据变异的因素称为自变量，受自变量影响的因素称为倚变量，相关关系的数量表达式即为回归方程。
一元线性回归 只有一个自变量x和依靠变量y的线性数学模型回归分析。通过试验或调查占有N对x_a、ya配对数据在x、y坐标上的散点较集中地分布在一条直线附近，可按一元线性回归模型进行统计分析，其数学模型为：

y_a＝β₀+β_x+ε_a (1)
α=1,2，…，N

式(1)中 观察值y是服从正态分布N(β₀+β_xa,σ)的随机变量，εa是服从正态分布N(0,σ)的随机变量并受∑ε=0条件的约束。x_a是可以严格控制或精确测量的一般变量。只有离所有散点距离最近的那条直线最能表示x_a与y_a的关系，可表示为：
y_a＝b₀+b_xa (2)
式(2)中 y_a为回归值（即计算值）。b₀称为纵轴截距，表示x=0时y的值。b称为回归系数，其取值大小可反映因素x对y作用的大小，b的正负号可反映因素x对y作用的方向。
观察值y_a与回归值ŷ之差刻划了各散点y_a与回归直线式(2)的偏离程度。式(2)中统计数b₀、b应在观察值y_a与回归值偏差(y_a-ŷ_a)的平方和Q(b₀、b)最小的前提下求得。其解为：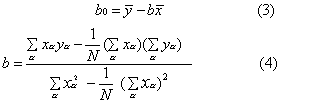

若F大于给定显著水平α下的临界Fa(1,N-2)，说明β=0的假设不成立，即为回归方程在α水平下是显著的。反之则为不显著，即β=0假设成立。
通过显著性检验的回归方程可以用于预报与控制。
有重复的一元线性回归 试验重复m次，共获得Nm个观察值，其数学模型为：
＝β₀+β_xa+ε (10)

α=1,2，…，N;i=1,2，…，m

式(10)中 参数β₀、β的最小二乘估计b₀同式(3),b为：

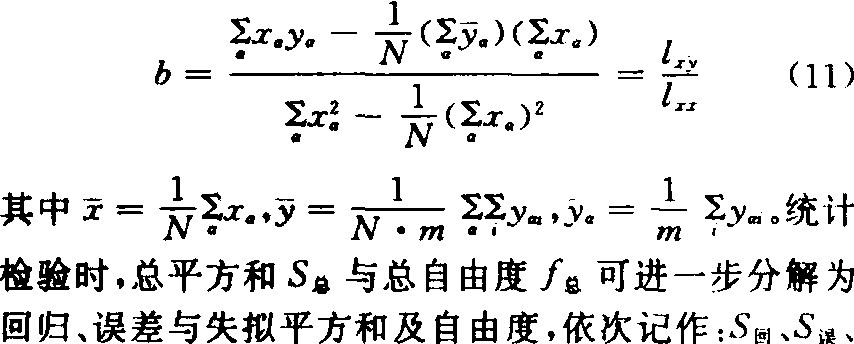
S_tf、f回、f误、f_tf。失拟平方和与误差平方和之和即为剩余平方和。重复试验提供的是真正的试验误差。失拟平方和是除了试验因素和误差以外的其他因素所造成的数据波动。它包括数学模型不当所造成的模型误差及其他未控因素的影响。这些影响也造成测定值与回归值的偏差，所以称为失拟平方和。在假设β=0成立的条件下，先作统计量F₁:

若对给定显著水平α下，F₁≤F_a说明失拟平方和基本上是误差引起，这时将失拟平方和与误差平方和合并为剩余平方和，将失拟自由度与误差自由度合并为剩余自由度，再作统计量F₂:

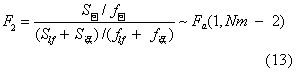
对给定显著水平α下F₂>F_a，则回归方程在该显著水平下显著。若F₂≤F_a，则因素x对测定值y的影响不显著或是试验误差过大，不能判定因素x是否显著地影响测定值y。
若给定显著水平下F₁>F_a，说明除试验因素外，还有其他因素也影响着测定值y的取值，这时作统计量F₃:

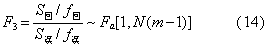
若在给定显著水平a下F₃>F_a，说明因素x对测定值y是有显著影响的，但还存在其他有影响的因素，回归方程的拟合不会很理想。但也可能是线性回归模型不适合，可试配合其他形式的曲线回归。若不能改善拟合效果，下一轮试验应从专业角度修改试验方案或增加其他试验因素。若F₃≤F_a则可能是因素x对观察值y的影响不显著，或者是误差过大所造成。
部分处理设重复的回归方程 不设重复试验的实验单元数为N个，设置m次重复后实验单元数为Nm个，工作量增加m倍。若只对第N个处理设置m次重复，则试验的实验单元数为N+m-1。线性回归模型为：
y_a＝β₀+β_x+ε_a。(15)
α=1,2，…，N-1,N,N+1，…，N+m-1
其平方和与自由度的分解的项数与有重复的一元回归一样，但误差平方和只用有重复的第N个处理求得。进行平方和与自由度分解后，即可做F₁、F₂、F₃的统计测验。
多元线性回归 见多元回归。
回归分析已经成为农业化学研究的重要技术，几乎在农业化学的所有领域都有应用。

线性回归linear regression

回归分析中，自变数均为一次的回归方程。当自变数单个时，称一元线性回归或直线回归。当自变数有两个和两个以上时，称多元线性回归。

线性回归

见“回归分析”条。

线性回归linear regression

与曲线回归相对，用直线表示的回归。若因变量Y对自变量X₁、X₂…、Xp的回归方程是一线性方程，即μ_y＝β₀ +β₁X₁ +β₂X₂ +…β_pX_p，其中β₀是常数项，β_i是自变量X_i的回归系数，P为任何自然数。这时就称Y对X₁、X₂、…、X_p的回归为线性回归。