突变论

指从原有形态结构突然变为新的形态结构的不连续过程。荷兰植物学家、遗传学家德佛里斯根据月见草突然发生显著变异的现象所提出的一种进化学说。认为新物种是通过不连续的偶然的显著变化而出现的。突变包括染色体畸变、基因突变、细胞质突变。德佛里斯所指的突变主要是染色体畸变。基因突变是更为普遍和更为基本的突变。突变的实质是在外界理化因素或体内某些诱变因素的作用下，DNA分子上某些碱基发生变化，改变碱基配对作用。基因突变一般具有偶发性、多向性、可逆性，有害性等基本特征。20世纪70年代初法国数学家托姆创立的数学分科也称“突变理论”。突变论用拓扑学、奇点理论和结构稳定性理论，为解释和预测现实中发生的不连续的或“突然的”变化过程，提出了一些数学模型。基本突变有折叠形突变、光点形突变、燕尾尾形突变、蝴蝶形突变、双曲脐形突变、椭圆脐形突变、抛物脐形突变等7种。突变理论可广泛地运用于物理、工程、力学、化学、生物学、心理学、精神病学、语言学、经济学、社会学等等方面。桥梁的坍陷、细胞的分裂、友谊的破裂、市场的破坏、社会结构的激变等，都是突变论的研究对象。

突变论tubianlun

描述突变现象的一般理论。对任何一个系统，其状态的变化可以分为两种类型，一种是连续的渐变，如牛顿力学中常提到的匀加速直线运动，另一种是不连续的、跳跃式的突变，如一定质量的气体在一定的温度和压力之下会变成液体，地壳的剧烈运动引起地震等等。以往我们处理问题的数学工具基本上是以微积分为基础的，系统的状态通常满足一组微分方程，由于微分方程的解必须是可微分的函数，所以它适合于描述连续的渐变的过程，对丰富多彩的突变现象就显得无能为力。60年代末法国数学家托姆(Thom)在当时奇点理论（数学的一个分支）发展的最新成就基础上提出了突变理论，从数学上对各种各样的突变现象进行了分类。突变论强调从整体上把握系统的性质，为研究系统的突变行为提供了新的思路。它处理问题的一般过程如下：
❶确定刻划系统宏观状态的变量(x₁,x₂，…，xn)，这些变量应反映系统所表现出来的宏观性质。
❷确定影响系统行为的控制参数(u₁,u₂，…，ur)。
❸系统的行为受某个依赖于(x₁,x₂，…，xn;u₁,u₂，…，ur)的函数P(x₁,x₂，…，xn;u₁,u₂，…，ur)所支配，在突变论中，这个函数称为势函数。
❹考察势函数的性质，就能够确定系统突变可能发生的范围。由于现实世界中的突变现象千姿百态。因此一般说来所谓的势函数可以非常复杂。但是托姆突变论的关于基本突变的分类定理指出，对于两个变量的系统尽管势函数P千千万万，但只要势函数中控制参量的个数r（称为余维）不超过4，那么突变方式在某种意义上只有7个基本类型，其它势函数通过变换可以化为这7种形式。下面就是这7种突变类型的名称，控制参量的个数r和一般的势函数的形式。

名称	余维r (控制 参量个 数)	函数形式
折叠型 尖点形 燕尾型 双曲脐点型 椭隧脐点型 蝴蝶型 抛物脐点型	1 2 3 3 3 4 4	x31+u1x1 x41+u1x21+u2x1 x51+u1x31+u2x21+u3x1 x31+x32+u1x1x2+u2x1+u3x2 x31-x1x22+u1(x21+x22)+u2x1+u3x2 x61+u1x41+u2x31+u3x21+u4x1 x21x2+x42+u1x21+u2x22+u3x1+u4x2

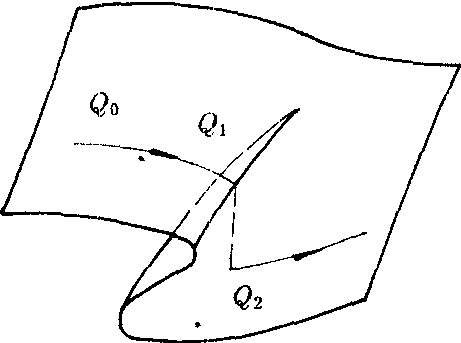
对于双变量系统只要控制参量的个数不超过4，我们就可以把决定系统状态的势函数化成上面7种类型之一，从而可以决定系统的行为曲面。如尖点型突变，它所对应的行为曲面如下图所示。假定系统的状态在外界参数的控制下从Q0向Q₁移动，到达悬崖边缘后，系统的状态就会掉到下半曲面的Q₂点上，这也就是系统状态的突变现象。

自从突变论在60年代末问世以来，其应用已遍及自然科学和社会科学各领域。总的来说，突变论的应用分为两类，一类是在力学、物理学等领域中的硬应用。另一类是在生物学、社会科学领域中的软应用，它使得我们可以讨论神经冲动传播、物种的兴衰、经济危机、战争爆发等各种突变行为。但像一切新理论的诞生发展一样，突变论（特别是它的应用）还须在实践中检验。修正与发展。

---

突变论tubianlun

一个新的数学分支。法国数学家雷内·托姆在1972年出版的《结构稳定性与形态发生学》一书奠定了该理论的基础。它以拓朴学为基础，从数学的角度研究各种事物在连续变化过程中的突然变化，为突变现象提供了数学模型。它在众多领域得到广泛运用。在物理学中突变论运用于相变、耗散结构的热力学等方面的研究，取得了显著成果。突变论的创始人对把突变论运用于生物学给予重大关注，企图用突变论为形态发生建立数学模型。他认为，生物体的生长可看是一系列渐变为生物化学上的突变所触发，并转而触发生物化学上的突变。根据这一思想，有些科学家已在这方面做出了许多有益的尝试。突变论在医学、化学、地质学、生态学以及社会科学领域也得到广泛应用。

突变论

数学的一个分支。运用拓扑学、奇点理论和结构稳定性等数学工具，研究自然界各种形态、结构和社会经济活动的非连续性突然变化现象的理论。

突变论

研究自然界和人类社会中存在的突变现象的学科。法国数学家托姆1972年发表的专著《结构稳定性和形态发生学》是这一学科建立的标志。突变论把人们关于质变的经验总结成数学模型，力求以统一的数学模型对这些突变加以描述、预测和控制。控制变量和状态变量是突变理论中的两个最基本的概念，前者是指那些作为突变原因的连续变化因素，状态变量是指可能出现突变的量。突变论着重探讨这两个变量之间的关系，用以说明自然界和人类社会中存在的大量不连续现象，如基因突变、地磁场倒转、经济危机、战争与和平等。突变论由于为突变现象提供了数学模型，现已被应用到物理学、生物学、医学、化学、地质学、生态学及社会科学等领域中，并取得了初步成果。

突变论Saltation

一种使用数学模型来描述临界点处外界环境变化引起系统质变的原理的方法。它与“耗散结构论”、“协同论”并称为“系统理论新三论”，已成为系统分析理论中的一个重要分支。突变论主要涉及的要素是临界点。例如在0℃，水由液态转变为固态，0℃就是临界点。突变论是在拓扑学、奇点理论和稳定性数学理论基础上发展起来的，现已广泛应用于流体力学、人口学、气象学等领域。

突变论

（一）荷兰植物学家、遗传学家德佛里斯根据月见草突然发生显著变异的现象所提出的一种进化学说。认为新物种是通过不连续的偶然的显著变化而出现的。现在知道，突变包括染色体畸变、基因突变、细胞质突变。德佛里斯所指的突变主要是染色体畸变。基因突变是更为普遍和更为基本的突变。突变的实质是在外界理化因素或体内某些诱变因素的作用下，DNA分子上某些碱基发生变化，改变碱基配对作用。基因突变一般具有偶发性、多向性、可逆性、有害性等基本特征。 （二）20世纪70年代初由法国数学家托姆创立的一个数学分科。又称“突变理论”。“突变”的基本含义是指从原有形态结构突然变为新的形态结构的不连续过程。突变论以此种现象作为研究对象。它用拓扑学、奇点理论和结构稳定性理论，为解释和预测现实中发生的不连续的或“突然的”变化过程，提出了一些数学模型。基本的突变有折叠形突变、光点形突变、燕尾形突变、蝴蝶形突变、双曲脐形突变、椭圆脐形突变、抛物脐形突变等7种。突变理论可广泛地运用于物理、工程、力学、化学、生物学、心理学、精神病学、语言学、经济学、社会学等等方面。桥梁的坍陷、细胞的分裂、友谊的破裂、市场的破坏、社会结构的激变等，都是突变论的研究对象。一般认为突变论为量变质变理论提供了一种新的数学模型。有人称之为20世纪的一次“智力革命”。

---

突变论

是通过描述在临界点的状态来研究系统非连续变化的数学理论。突变的英文是cacastrophe theory，意为突然的灾难。这一理论是法国数学家雷内·托姆在惠特内的“奇点理论”的基础上创立的。托姆把惠特内定理的应用命名为突变论。1972年，托姆出版了《结构稳定性和形态发生学》一书，系统地阐述了突变论。
突变论的研究内容可概括为：考察系统从一种稳定状态到另一种稳定状态的飞跃。从牛顿开始的经典物理学基本上是研究自然界渐变现象的理论，而突变论则是对突变过程的定性、定量的研究。突变论把系统所处的状态用一组参数描述。描述状态的量称状态变量，把引起突变的连续变化的量称控制变量。托姆指出，系统从一种稳定态近入不稳定状态，如果参数再略作变化，会使处于不稳定状态的系统近入另一种稳定态，在这时状态就发生了突变。突变论运用数学工具给出系统处于稳定态和不稳定态的参数区域。参数变化，系统状态也发生变化，参数通过某些特定位置时，状态就会发生突变。托姆通过严格推导得出一个结论：当控制变量少于4个时，自然界的各种突变可用7个数学模型描述。这7个基本突变方式按几何模型的形状称为：折迭型、尖点型、燕尾型、蝴蝶型、双曲型、椭圆型、抛物型。经数学证明，控制变量为两个时，最简单的突变都是尖点型。
现在，突变论已不同程度地应用于物理学、生物学、生态学。在以突变论研究社会事物方面还存在争议。我国哲学工作者根据突变论的稳定理论，提出了一个判定飞跃和渐变的原则：在严格控制的条件下，如果质变经历的中间状态是不稳定的，就是飞跃过程；如果中间状态是稳定的，就是一个渐变过程。从而回答了质变过程是“飞跃”，还是渐变的争论。数学家斯图尔特在《七种突变》一文中认为，突变理论已经站住脚根，但是它亦非万能。新闻与舆论中也存在突变现象，但如何应用突变论加以研究，还是个空白。

突变论

研究自然界和人类社会中连续渐变如何引起突变或飞跃，并力求以统一的数学模型来描述，预测并控制这些突变或飞跃的一门学科。它把人们关于质变的经验总结成数学模型，表明质量既可通过飞跃的方式，也可通过渐变的方式来实现，并给出了两种质变方式的判别方法，它还表明，在一定情况下，只要改变控制条件，一个飞跃过程可以转化为渐变，而一个渐变过程又可转化为飞跃。突变论认为事物结构的稳定性是突变论的基础，事物的不同质态从根本上说就是一些具有稳定性的状态，这就是为什么有的事物不变，有的渐变，有的则突变的内在原因。在严格控制条件的情况下，如果质变经历的中间过渡状态是不稳定的，它就是一个飞跃过程； 如果中间状态是稳定的，它就是一个渐变过程。控制变量和状态变量是突变论中的两个最基本概念： 那些作为突变原因的连续变化因素是控制变量，那些可能出现突变的量是状态变量。当控制变量不变时，状态变量处于稳定状态； 当控制变量变化时，状态变量也随之而变，一般是渐变状态； 当控制变量达到某一数值时，状态变量原有的稳态消失，则进入突变状态。类比是突变论的重要内容之一，突变论把通过周密观察、分析建立的完全定量化的、精确的数学模型所描述的突变称为典型突变，又把典型突变分为若干最基本的类型，它通过对某一突变现象与典型突变之间的同异比较，从而确定该突变的所属类型。突变论形成于20世纪70年代。1972年法国数学家勒内·托姆发表了专著《结构稳定性和形态发生学》，标志着这一学科正式问世。作为突变论创始人的托姆最初是从生物学中的细胞、胚胎开始其研究的，后来其他科学家又把这一理论推广到遗传、生态、社会等研究领域。突变论的应用范围很广，利用突变模型可说明许多突变过程，如火山爆发、大桥断裂、轮船沉没、岩石断裂、胚胎发育、癌变、战争、经济崩溃、城市兴衰等过程，进一步控制这些过程的突变，从而为人类造福。