积差相关系数
两个连续型变量的观察值间相关系数的一种计算方法,其计算公式如下:r=![]() (xi-x)(yi-y)
(xi-x)(yi-y)![]() (xi-x)2
(xi-x)2![]() (yi-y)2。常被应用于测验分数统计中。
(yi-y)2。常被应用于测验分数统计中。
积差相关系数
积差相关系数jichaxiangguan xishu
指描述两个连续变量之间线性关系程度的一种量数,一般简称为相关系数。当一个变量变大(或变小)时,另一个变量也随之变大(或变小),称为正相关;当一个变量变大(或变小)时,另一个变量随之变小(或变大),称负相关;当一个变量变大(或变小)时,另一个变量的变化无一定规律(即可能变大、也可能变小,而且变大、变小的机会相似),则称为零相关或无线性关系。
[例] 对6个学生进行四种测验,结果如下。试分析测验A与其他测验的关系。
| 测验 被试 | 测验A | 测验B | 测验C | 测验D |
| 1 2 3 4 5 6 | 35 33 32 30 29 28 | 60 58 56 55 53 52 | 52 53 55 56 57 59 | 93 98 91 90 95 96 |
测验A与其他测验的关系图示如下:
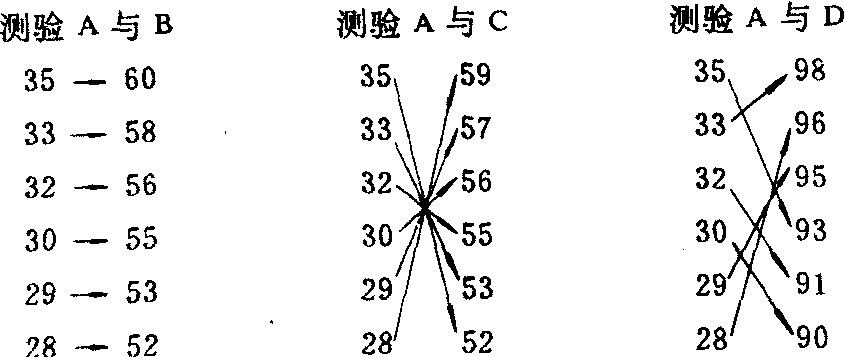
正相关(r=0.99) 负相关(r=-0.98) 零相关(r=-0.07)
积差相关系数的计算公式,实为两种标准变量之积的平均值,即
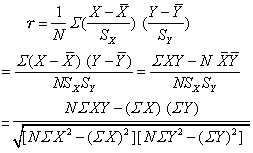
式中 N——数据的对数
、
 和SX、SY——两变量的平均数和标准差
和SX、SY——两变量的平均数和标准差ΣXY——两变量乘积之和
ΣX——变量X之和
ΣX2——变量X的平方之和
ΣY ——变量Y之和
ΣY2——变量Y的平方之和
应依数据的已知条件来采用适当的公式。若已知

相关系数的范围为:-1≤r≤1。在计算相关系数时,应以两变量之间含有某种关联为前提条件。此外,由于不同相关系数是用不同单位度量的,因而它们不能作加、减、乘、除的运算。
那么,我们怎样知道所计得的相关系数的关联程度呢?这需要作统计检验。检验的方法是查“检验相关系数显著性的临界值表”,该表中在自由度f=N-2及小概率α条件下,给出了r显著性的临界值r(f)α。当|r|≥r(f)α时,r有明显的相关关系(当α=0.05时,r为一般显著的相关关系;当α=0.01时,r为极显著的相关关系);否则,就认为r无显著意义。在上例中,因N=6,故f=N-2=4,在α=0.01时从“检验相关系数显著性的临界值表”中,可查到r(4)0.01=0.9172;由于r=0.99>r(4)0.01,故所计得的r为极显著的相关关系。
☚ 相关量数 偏相关系数 ☛
积差相关系数
积差相关系数product moment coefficientof correlation
表示两个连续变量X和Y之间相关联程度的统计量。它表示一个变量伴随着(或独立于)第二个变量的变化范围。用rxy或r表示。因它是根据英国统计学家皮尔逊提出的积差法而计算的相关系数,所以也称皮尔逊相关系数。其基本计算公式为:
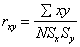
式中x为X数列各量数与其平均数之差,y为Y数列各量数与其平均数之差,Sx,Sy分别为X和Y数列各变量的标准差,N为各对量数的总数。如将上式中的N消去,则得一简便公式如下:
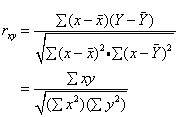
☚ 机械识记 激情 ☛
- 新诗惠我,开卷醒然欣再读。是什么意思
- 新诗戏剧化是什么意思
- 新诗改罢自长吟。是什么意思
- 新诗日日成,不是爱名声;旧句时时改,无妨悦性情。是什么意思
- 新诗时向梦中得,明月多从枕上看。是什么意思
- 新诗欲飞动,病眼为开明。是什么意思
- 新诗歌是什么意思
- 新诗歌会是什么意思
- 新诗歌派是什么意思
- 新诗歌的斯达哈诺夫运动是什么意思
- 新诗歌社是什么意思
- 新诗淡似鹅黄酒,归思浓如鸭绿江。是什么意思
- 新诗源是什么意思
- 新诗满轴频舒卷,薄酒盈樽自醉醒。是什么意思
- 新诗潮是什么意思
- 新诗潮社是什么意思
- 新诗点检留心苦,旧事寻思觉鼻酸。是什么意思
- 新诗用韵手册是什么意思
- 新诗略谈是什么意思
- 新诗的“顿”是什么意思
- 新诗的写作手法是什么意思
- 新诗的标点是什么意思
- 新诗的格调及其它是什么意思
- 新诗的浪漫主义思潮是什么意思
- 新诗的现代主义思潮是什么意思
- 新诗的现实主义思潮是什么意思
- 新诗的结胎是什么意思
- 新诗社是什么意思
- 新诗见久要,清论激深衷。是什么意思
- 新诗豹变莺藏后,好梦龙飞凤舞来。是什么意思
- 新诗鉴赏1是什么意思
- 新诗鉴赏10是什么意思
- 新诗鉴赏11是什么意思
- 新诗鉴赏12是什么意思
- 新诗鉴赏13是什么意思
- 新诗鉴赏14是什么意思
- 新诗鉴赏15是什么意思
- 新诗鉴赏16是什么意思
- 新诗鉴赏17是什么意思
- 新诗鉴赏18是什么意思
- 新诗鉴赏19是什么意思
- 新诗鉴赏2是什么意思
- 新诗鉴赏20是什么意思
- 新诗鉴赏21是什么意思
- 新诗鉴赏22是什么意思
- 新诗鉴赏23是什么意思
- 新诗鉴赏24是什么意思
- 新诗鉴赏25是什么意思
- 新诗鉴赏26是什么意思
- 新诗鉴赏27是什么意思
- 新诗鉴赏28是什么意思
- 新诗鉴赏29是什么意思
- 新诗鉴赏3是什么意思
- 新诗鉴赏30是什么意思
- 新诗鉴赏31是什么意思
- 新诗鉴赏32是什么意思
- 新诗鉴赏33是什么意思
- 新诗鉴赏34是什么意思
- 新诗鉴赏4是什么意思
- 新诗鉴赏5是什么意思