秦九韶1202—1261

南宋数学家。字道古，普州安岳（今属四川）人。祖籍山东。早年侍亲于金之中都，因得访习于太史，又曾在杭州从隐者受数学。及长，寓居湖州。精研星象、音律、算术以至营造等事。淳祐七年(1247年)，著《数书九章》十八卷，书中阐发贾宪“增乘开方法”（求高次幂的正根法），解一个一元十次方程式，并附有算图。算图中列算式如层层剥笋，秩序井然，至今仍有人称“增乘开方法”(又称“正负开方术”)为“秦九韶程序”。他曾发明整数论中一次同余式组的普遍解法(即“大衍求一术”)，此即闻名世界的“中国剩余定理”。后因精历学被荐于朝廷，知琼州（广东琼山县）、梅州（广东梅县），卒于梅。

秦九韶

中国数学家。生于约1202年，卒于约1261年。其主要成就是系统地总结和发展了高次方程数值解法和一次同余组解法，提出了相当完备的“正负开方术”和“大衍求一术”，达到了当时世界数学的最高水平。此外，他对天文历法也颇有研究。时人评论他“性极机巧，星象音律算术以至营造等事，无不精究”(宋·周密《癸辛杂识》)。

149 秦九韶约1202一约1261

南宋数学家。宋元数学四大名家之一。字道古，普州安岳(今四川安岳县)人。生活于元兵南侵的战乱年代。曾任县尉、通判、郡守、知府等。1224年随父到京都(今杭州)向名师学习数学、天文。他博学多才，“性极机巧，星象、音律、算术以至营造(即建筑)等事无不精究”(《畴人传》)。潜心钻研数学，总结前人经验。注意从社会生产、生活各领域搜求数学问题，“设问为答，以拟其用”(《畴人传》)，于1247年完成杰作《数书九章》。他在《孙子算经》的“物不知数”问题基础上，总结了历算家推算上元积年的方法，提出了系统、完整的一次同余式组的理论与方法——大衍求一术。针对各种情况给出了相应的程序。集贾宪、刘益等人之大成，提出了以增乘开方法为主导的求高次方程正根的方法——正负开方术。将贾宪开创的增乘开方法发展到十分完备的地步。他发展了刘徽求微数的思想，在世界数学史上第一次用十进小数表示无理根的近似值。彻底改进了线性方程组解法，以互乘相消法代替了“直除法”，并在互乘前约去公因子，使运算更加简便。在解题中已用到相当于增广矩阵的初等变换。提出了根据三角形三边长求面积的“三斜求积公式”。在方程论和一次同余理论研究两大领域内取得了超越前人的丰硕成果。为中国古典数学的发展作出重大贡献，在世界数学史上占有重要地位。欧洲直到18-19世纪才由欧拉(L.Euler,1707—1783)和高斯(C.F.Gauss,1777—1855)对一般的同余式组解法进行深入研究，在秦九韶之后500余年重新得到同样的成果。

秦九韶Qin Jiushao，约1202—约1261

南宋数学家.其名著《数书九章》(1247)包括下列杰出的成就.
❶勾股测量问题的系统研究.

❷任意三角形的 “三斜求积”公式

与希腊海伦公式等价.

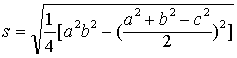
❸大衍总数术，即一次同余式组解法，这在中国至少可以上溯到汉代历法中上元积年的推算. 秦九韶从理论上作出辉煌总结，将问题推广到一般情形，即相当于求满足

N≡R_i (modA_i) (1)

的所有N中的最小正整数解，A_i为任意正有理数，i=1,2，…，n.
解法分两部分：
其一，将A_i化为两两互紊的正整数 {a₁,a₂ ，…，a_n)，满足a_i|A_i; (a_i, a_j) =1 (i≠j)及 a_i＝ [A₁, A₂,i=1 …，A_n](最小公倍数，若A.非整数，则先化为整数).于是同余式组化为等价的N≡r_i (modai) i=1,2，…，n. (2)
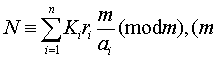
其二，通过剩余定理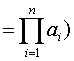求N，这里K_i是满足kim/ni≡1 (modai)的正整数(i=1,2…，n)，称为乘率，求k i的算法称为“大衍求一术”. 秦九韶给出了这样十分精巧的算法程序，在欧洲，经欧拉、拉格朗日、高斯三代大师的探索才达到相同水平，已在秦九韶之后550多年了.

❹正负开方术，即高次方程数值解法. 秦九韶给出了统一、完整的算法程序，至今仍常被使用. 欧洲直到鲁斐尼 (1804)、霍纳 (1819)才达到相近水平，而且解法远不如秦九韶的方法井然有序. 美国科学史家萨顿认为，秦九韶是“他那个民族，他那个时代，并且确实也是所有时代最伟大的数学家之一.”

秦九韶约1202——约1261Qinjiushao

中国数学家。生活于南宋后期，精通数学、天文历法、音乐及建筑。他的数学名著《数书九章》(1247)中有许多创造性的工作， 最重要的是以下几项：
对勾股测量问题的系统研究。
独立地得到了关于任意三角形面积的 “三斜求积
大衍总数术，即一次同余式组解法(参见“物不知数”)。任给同余式组N≡R_i (modAi), 其中A_i为任意正有理数 (i=1, 2, …， n), 秦九韶给出了求最小正整数解N的一个完整而精巧的一般方法。
正负开方术，即高次方程数值解法，对于任意的数值多项式方程
f(x)=a_nxⁿ+an-₁x^n-1+…+a₁x+a₀＝o
秦九韶给出了求正根的一个步骤明确， 求解迅速的一般演算程序， 并且用求解一个10次方程显示了他的方法的优越性。
为了理解后两项成就有多么重要， 只需要指出以下事实就够了：
在欧洲，一次同余式组的完整解法经过欧拉、拉格朗日、高斯三代大师的探索，到19世纪初才达到与秦九韶解法相同的水平。
关于高次方程，阿拉伯数学家卡西(al-Kashi)于1427年重复了秦九韶的工作，欧洲直到19世纪初才由意大利鲁斐尼Ruffini,1804)、英国霍纳Horner,1819)发表水平相当的解法，却远不如秦九韶的方法井然有序。
秦九韶生在四川，青少年时曾随做官的父亲在南宋首都临安（今杭州）生活过几年，得到了在天文、历法、数学等方面向专职人员请教的机会，并且从一位隐士那里学到不少数学知识。同时代人曾说：“九韶性极机巧，星象、音律、算术以至营造等事无不精究。迩尝从李梅亭学骈俪诗词，游戏、毯马、弓剑莫不能知”，可见他是何等多才多艺，后来他曾担任过几次下级官吏。由于蒙古军南下，战乱连年，加之官场失意，情绪不免低落。他却能在“尝险罹忧”之中，穷十年之功精研数学，写成洋洋二十万言，创造多项成就的杰作《数书九章》，并因此赢得了世界性的声誉。美国著名科学史家萨顿(Sarton.G.)认为，秦九韶是“他那个民族、他那个时代，并且确实也是所有时代最伟大的数学家之一。”

秦九韶约13世纪

中国南宋数学家。把贾宪的增乘开方法推广为正负开方术（数字高次方程的求正根法），用大衍求一术（初等数论中一次同余式组解法）完满解决了“孙子问题”。著《数术九章》。

秦九韶

南宋数学家。字道古。生于四川，祖籍山东，自称鲁郡人。青年时期，曾在临安(南宋首都，今杭州)太史院学习数学。淳佑七年(1247年)著《数书九章》18卷。对“大衍求一术”（整数论中的一次同余式解法）和“正负开方法”（数字高次方程的求正根法），有卓越的研究成果。前者称“中国剩余定理”，后者称“秦九韶程序”。

秦九韶

南宋数学家。淳祐七年(公元1247年)著有《数书九章》十八卷。对于“大衍求一术” （整数论中的一次同余式解法）和“正负开方术” （数字高次方程的求正根法）等都有深入的研究。