祖暅原理
052 祖暅原理
即刘祖原理。见32051。
☚ 刘祖原理 圆周率 ☛
祖暅原理
祖暅原理zugeng yuanli
夹在两个平行平面间的两个几何体，若被平行于这两个平面的任何平面所截得的两个截面的面积都相等，则这两个几何体的体积相等.
如图中的两个几何体，若被平行于平面a的任何平面截得的两个截面的面积都相等，即五边形A1B1C1D1E1的面积=△P1Q1R1的面积，五边形A2B2C2D2E2的面积=△P2Q2R2的面积等等，则这两个几何体的体积相等.
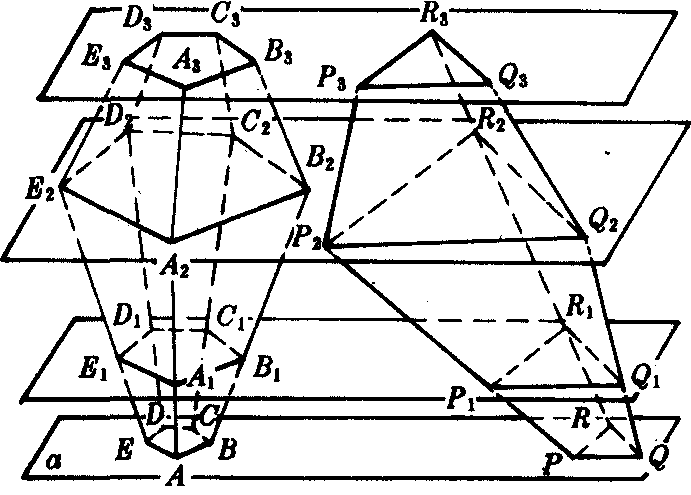
这个原理在高等数学中是可以证明的.我国古代的数学家祖暅（祖冲之的儿子）在公元5世纪就早已提出了这个原理，把它作为公理用.祖暅原理的原文是“幂势既同，则积不容异”，“幂”是截面积，“势”是几何体的高，意思是：两个同高的几何体，若与底等距离的截面积总相等，则几何体的体积相等.在欧洲，直到17世纪，意大利数学家卡瓦利里才提出这个命题.祖暅发现这一原理比卡瓦利里要早一千多年.
☚ 长方体的体积 棱柱的体积公式 ☛
- 意林2018年-26是什么意思
- 意林2018年-27是什么意思
- 意林2018年-28是什么意思
- 意林2018年-29是什么意思
- 意林2018年-3是什么意思
- 意林2018年-30是什么意思
- 意林2018年-31是什么意思
- 意林2018年-32是什么意思
- 意林2018年-33是什么意思
- 意林2018年-34是什么意思
- 意林2018年-35是什么意思
- 意林2018年-4是什么意思
- 意林2018年-5是什么意思
- 意林2018年-6是什么意思
- 意林2018年-7是什么意思
- 意林2018年-76是什么意思
- 意林2018年-77是什么意思
- 意林2018年-78是什么意思
- 意林2018年-79是什么意思
- 意林2018年-8是什么意思
- 意林2018年-80是什么意思
- 意林2018年-81是什么意思
- 意林2018年-82是什么意思
- 意林2018年-83是什么意思
- 意林2018年-84是什么意思
- 意林2018年-85是什么意思
- 意林2018年-86是什么意思
- 意林2018年-87是什么意思
- 意林2018年-88是什么意思
- 意林2018年-89是什么意思
- 意林2018年-9是什么意思
- 意林2018年-90是什么意思
- 意林2018年-91是什么意思
- 意林2018年-92是什么意思
- 意林2018年-93是什么意思
- 意林2018年-94是什么意思
- 意林2018年-95是什么意思
- 意林2018年-96是什么意思
- 意林2018年-97是什么意思
- 意林2018年-98是什么意思
- 意林2018年-99是什么意思
- 意林-21是什么意思
- 意林-22是什么意思
- 意林-23是什么意思
- 意林-24是什么意思
- 意林-25是什么意思
- 意林-26是什么意思
- 意林-27是什么意思
- 意林-28是什么意思
- 意林-29是什么意思
- 意林-3是什么意思
- 意林-30是什么意思
- 意林-31是什么意思
- 意林-32是什么意思
- 意林-33是什么意思
- 意林-34是什么意思
- 意林-35是什么意思
- 意林-36是什么意思
- 意林-37是什么意思
- 意林-4是什么意思