百分位数

一种特殊的分位数，对应于α=0.01,0.02，…，0.99的α分位数。常被应用于测验分析统计中。

百分位数baifen weishu

亦称百分位点。指用百分比来表示某数据所处地位的一种量数，一般用符号Pm表示。如P₇₅，表示第75个百分位点的一个数，这点以下的数据占全部数据的75%。前面介绍过的中位数，实际上就是第50百分位数。故对未分组数据计算百分位数时，可参考计算中位数的方法(即把数据排序后，用N^m/100求第m百分位点的位置，N为数据总个数)。
对已分组数据，用下式计算百分位数：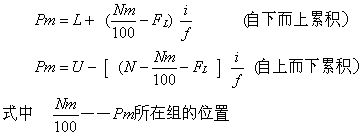

L——Pm所在组的精确下限
FL——小于L的累积次数
U——Pm所在组的精确上限
FU——大于U的累积次数
i ——组距
f——Pm所在组的次数
[例] 在下表中求P₇₅。

组距	次数	自下而上的 累积次数	自上而下的 累积次数
81～90	2	145	2
71～80	20	143	22
61～70	33	123	55
51～60	40	90	95
41～50	29	50	124
31～40	12	21	136
21～30	8	9	144
11～20	1	1	145

第一步，在自下而上的累积次数中，依或P₇₅所在组，即145×75/100=108.75；比它略大的组为61～70，即为P₇₅所在组。
第二步，依公式计算P₇₅＝60.5+ (108.75-90)1^0/33＝66.2
用上述两个公式所计得的结果是一致的。
百分位数可以准确地表明某百分位所对应的分数。它可用于依一定的百分率来判定具体的录取分数线；也可对不同总体的学生成绩进行位置比较。
此外，可用百分位数之间的差距（称为百分位差）作为描述数据的离中趋势的一种量数，如四分位差、十分位差等。四分位差(Q)的计算公式为

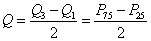
式中 Q₁——第1个四分位数
Q₃——第3个四分位数(Q₂＝P5₀为第2个四分位数，即为中位数)
同理，十分位数(Di)与百分位数的对应关系如下：D1=P10,D₂＝P₂₀,D₃＝P₃₀，…，D9=P90。其中前后相应的2个十分位数之差(如P₉⁰-P₁₀)就是十分位差。

百分位数percentile

是将某一组变量值从小到大依次排列，然后分成100等份，与某一个等份相对应的变量值即为某百分位数，用P_x表示，x代表某一等份。如第百分之五位数用P₅表示，第百分之九十五位数用P₉₅表示。统计上常用百分数来说明偏态分布或分布不清资料的离散情况。使用百分位数时，要求资料的例数不要过少，否则靠近两端的百分位数不稳定。

百分位数

百分位数是一种位置指标，以符号Px表示。一个百分位数将总体或样本的全部观察值分为两部分，理论上有x%的观察值比它小，有(100-x)%的观察值比它大。如含量为n的样本，取第5百分位数P5，理论上有n×5%个观察值比P5小，有n(100-5)%个观察值比P5大，故百分位数是一个界值。它的计算方法有频数表法和图解法。
对于某一连续的分布函数，当指定x%后，Px即为定值； 而对于一组原始数据如100例由小到大排列的正常成人发汞值(μg/g): 2.2,2.3，…，2.6,2.7,2.8,3.0,4.0,4.3，其P₉₅不是恰等于某一观察值，只能说P₉₅在2.6与2.7之间，因为任何介于2.6与2.7之间的数，都具有95%的观察值比它小，5%的观察值比它大的特性。当P₁,P₂,P₃，…，P99确定后，一个由小到大的有序数列即被分为100等份，各含1%的观察值，所以百分位数也就是该序列的百等份分割值。
统计上某些其他的分割值与相应的百分位数等价。如中位数(1883年F. Galton首用此名)将一序列的全部观察值二等分，上下各有1/2的观察值，与P50等价。四分位数将一序列的全部观察值四等分，各有1/4的观察值，其第1四分位数（亦称下四分位数）、第2四分位数（即中位数）、第3四分位数（亦称上四分位数）依次与P25,P50,P75等价。十分位数将一序列的全部观察值十等分，各有1/10的观察值，其第1十分位数，第2十分位数，……，第9十分位数，依次与P10,P20，…，P90等价。这些分割值都可按求百分位数的方法来计算。
百分位数的用途是：
❶描述一组资料（样本或总体观察值）在某百分位置上的水平。
❷百分位数就是分布数列的百分界值，表示它的上下各有百分之几的观察值，常用于确定医学正常值以及身体发育水平等的界限。
❸在假设检验中用作拒绝或不拒绝检验假设的界值。
❹用一组百分位数，如P₅,P₂₅,P₇₅,P₉₅，可以描述总体或样本的分布特征，包括位置值的大小和变异度。
百分位数并非由全部观察值综合计算得来，因此它不如均数和标准差精确； 然而中间部分的百分位数因不受资料中个别极端数据的影响，具有较好的稳定性。但靠近两端的百分位数，只在样本含量足够大时才比较稳定，因此，当样本含量不够大时，不宜取太近两端的百分位数。至于样本含量过少时，“百分”位数已经名不符实，应用价值也就很小了。
频数表法 步骤：
❶将观察值编制频数表；
❷按所分组段，由小到大累计频数，至略小于nx%为止；
❸按式(1)求P_x。

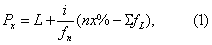
式中fx为nx%所在组段的频数，i为该组段的组距，L为其下限，∑fL为小于L各组段的累计频数。若上述第
❷步按所分组段由大到小累计频数，至略小于n(100-x)%为止，则改用式(2)求P_x。

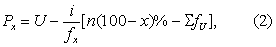
式中f_x为n(100-x)%所在组段的频数，i为该组段的组距，U为其上限，∑fU为大于U的各组段的累计频数。同一频数表资料由式(1)或式(2)算得的结果相等，因为式(1)式(2)都是根据补插法原理，两个补插的“点”在理论上应重合。应用时，当Px的x<50时用式(1)较方便，x>50时用式(2)较方便。
图解法 步骤：
❶将观察值编制频数表；
❷求累计频数及累计频率(%)如表第(4)、(5)栏；
❸在方格坐标纸上，以横轴表示频数表的组段，纵轴表示累计频率，依累计频率连成线图；
❹从纵轴上累计频率x%处作一水平线与图中折线相交，过交点作垂线交于横轴，此处的横坐标即所求百分位数 （如图）。图解法用图示代替补插计算，道理相同，但一般不及计算准确。由图可见，特别是靠近线的尾端较平坦部分，准确性较差。如果仅作粗略估计，尤其同时要估计多个百分位数时，用图解法颇方便。
例 某种沙门菌食物中毒患者164例的潜伏期见表第 (1)、(2)栏，求其95%分位数。
潜伏期P₉₅的计算

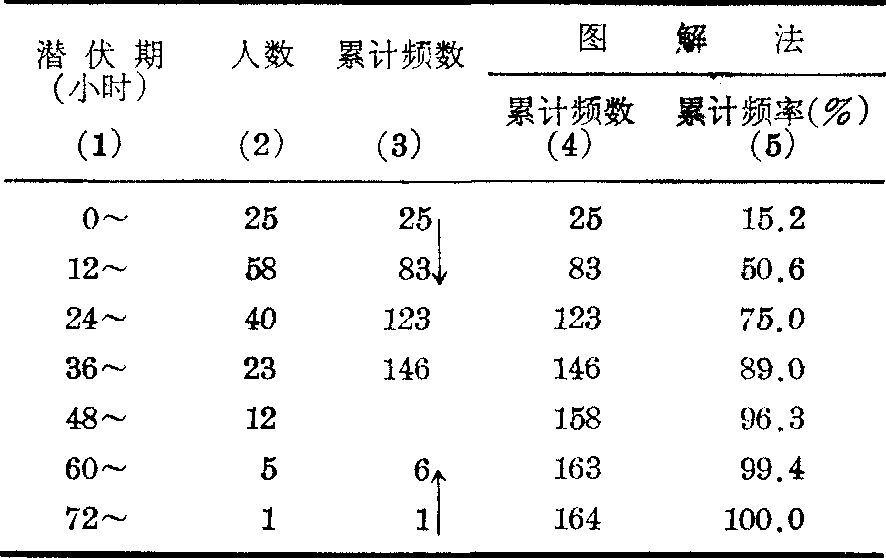
(1)频数表法： 求P₉₅时，x=95>50，按式(2)计算较方便。n(100-95)%=164(100-95)%=8.2，依组段由大到小的方向累计频数，见表第(3)栏下部，至略小于8.2为止，可见8.2在“48～”组段内，得fx=12,i=12,U=60,∑fu=6，代入式(2):

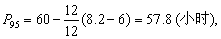
得此次食物中毒潜伏期的第95百分位数为57.8小时。
本例若按式(1)计算，依组段由小到大的方向累计频数，至略小于n(95%)=164×95%=155.8为止，见表第(3)栏上部，代入式(1):

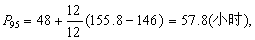
结果相同。
(2) 图解法： 先求累计频数及累计频率，见表第(4)、(5)栏，再将第(1)、(5)栏数据作图，得折线（见图）。于纵轴95%处作水平线，交于折线，从交点作垂线，目测其与横轴交点的横坐标约58小时，即所求P₉₅。

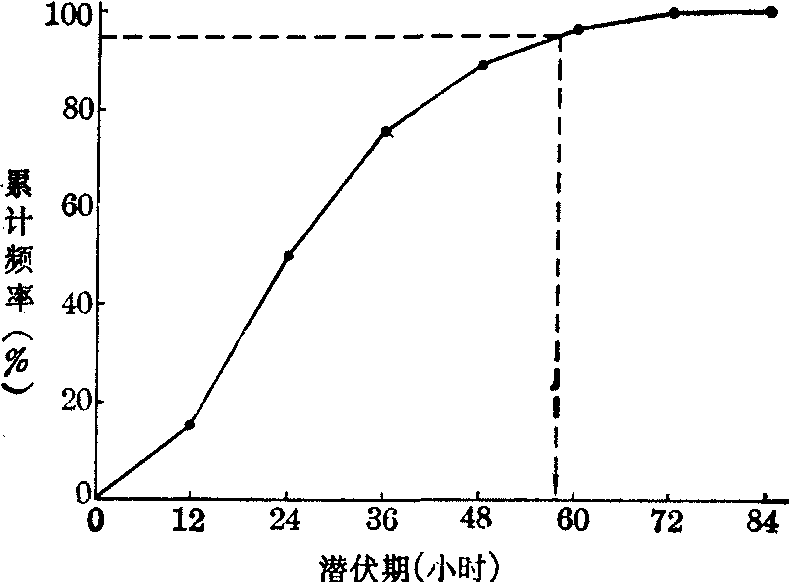
图解法求百分位数