理想气体状态方程lixiang qiti zhuangtai fang-cheng

习惯上称气态方程。理想气体是人们假想的，这种气体在分子间没有相互作用力，分子本身不占体积。一定质量的理想气体在始态时的压力、体积、热力学温度分别是p₁,V₁,T₁，经过某一变化过程到终态时分别变成p₂,V₂,T₂，气体从始态到终态、可以经过不同变化途径，设想经过一个等温过程，再经过一个等压过程。在第一个变化过程中，温度T₁保持不变，压力从p₁变成p₂，体积从V₁变成V_a，根据玻意耳定律： 恒温时，一定质量的气体，体积与它承受的压力成反比p₁V₁＝p₂V_a 或

在第二个变化过程中，当压力P₂保持不变时，温度从T₁变成T₂，体积从V_a变成V₂，根据盖·吕萨克定律： 恒压下，一定质量的气体，它的体积与热力学

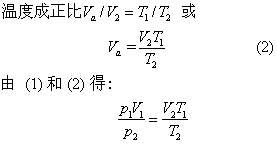
或

上式说明一定质量的理想气体，从始态(p₁,V₁,T₁)变到终态(p₂,V₂,T₂)，压力和体积的乘积跟热力学温度的比值是一个常数：

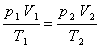
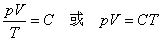
1mol任何理想气体在标准状态下(p₀＝1.013×10⁵Pa,T₀＝273K,V₀＝22.4L)的气体常数R=p₀V₀/T₀，将nmol理想气体（标准状况）占有的体积v₀＝nV₀代入上述气体状态方程可得

(3)式称理想气体状态方程，又称克拉珀龙方程，式中R叫做摩尔气体常数。标准状况下(p₀＝1.013

只要温度不太低，压力不太高，上述方程对一切气体都适用。常用摩尔气体常数值见表。

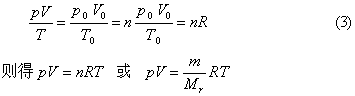
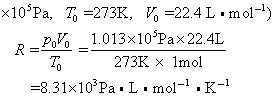
摩尔气体常数的单位和数值

p	V	T	n	R
帕(Pa)	升(L)	开(K)	摩尔(mol)	8.31×103 Pa·L·mol-1·K-1
帕(Pa)	米3(m3)	开(K)	摩尔(mol)	8.31 Pa·m3mol-1·K-1=8.31J·mol-1·K-1
大气压*	升 (L)	开(K)	摩尔(mol)	0.082 atm·L·mol-1·K-1
大气压*	毫升 (mL)	开(K)	摩尔(mol)	82 atm·mL·mol-1·K-1
毫米汞柱*	毫升 (mL)	开(K)	摩尔(mol)	62359 mmHg·ml·mol-1·K-1
达因·厘米-2* dyn·cm-2	厘米3(cm3)	开(K)	摩尔(mol)	8.31×107 erg·mol-1·K-1

* 现已禁用