熵

 源自希腊语tropie（变化），为克劳修斯（R.J.E.Clausius1822—1888）所创。1850年，28岁的德国物理学家克劳修斯认真总结了卡诺等人对热机研究的成果，首次提出了热力学第二定律，将其表述为热量不能自动地从低温物体流向高温物体。经过十五年的努力，他为这一定律构造出一个数学函数：ds=dQT。他写道：“如果我们想用一个专门的词来表示s，我们可以说它为物体的变换容度……，我建议称s为物体的entropy（熵），这个字来自希腊词ητροπη，即转变之意。我有意把字拼为entropy，以便与entropy（能量）尽可能地相似，因为这两个字所表示的量，在物理上都具有重要的意义，而且关系密切，以致在名词上相似，我认为是恰当的。”“熵”的概念就这样产生了。
 熵在宏观上是指一切自发过程总是一步一步地向着平衡态变化的；同时，系统的熵也在一步一步地增大。当系统达到平衡态时，其熵便不再增增加而达到最大，所以系统的熵越大，则说明它接近平衡态。换句话说，熵的大小反映了系统接近平衡的程度。因此，从宏观意义上讲，熵是系统接近平衡态的一种度量。
 熵这个概念被引入中国是在1923年，I.R.普朗克来中国讲学，物理学家胡刚教授为其做翻译，首次将德文“Entropie”译为“熵”。胡刚根据公式ds=ddQT，认为s为热量与温度之商，而且这个概念与火有关（象征着热），于是在商字上加火旁，构成新的汉字“熵”。
 泛化。各种各样的“熵”在各个学科里似乎以指数形式增长。在各种不同学科中，产生了许多数不清和说不清的“熵”的概念，如：地理熵、气象熵、生命系统熵、农业系统熵、社会熵、经济熵、文化熵、人体熵、精神熵、思维熵，以及泛系熵、泛熵、超熵、广义熵等等。
 “熵”这个概念一经出现，就受到许多蜚声世界科坛的科学权威的青睐。这些声名显赫的科学巨匠包括玻耳兹曼、爱因斯坦、爱丁顿、薛定谔、申农、维纳、贝塔朗菲、布里渊、普利高津、哈肯……其中有不少是诺贝尔奖的获得者。在克劳修斯之后，大科学家们为熵理论呕心沥血百余年。
 熵作为一个基本概念被引入热力学，带来科学的深刻变化，拓展了物理领域。1877年，玻耳兹曼熵统计学的解领域。1877年，玻耳兹曼熵统计学的解释，大大丰富了其物理学的内涵，明确了它的应用范围。1929年，西拉德又发现了熵与信息的关系，揭示了熵含意的新层次，进一步扩大了熵的应用面。目前，不仅在自然科学与工程技术的许多领域会发现熵的踪迹，就是在社会科学与人文科学的书籍与文章中，也经常会碰到熵这一名词，由于熵的概念比较抽象隐晦，它既然广泛地为人们所应用，也就难免为有些人所滥用。
 纵观“熵”概念提出的一百多年的历史，熵的概念层出不穷，数不胜数，但大都来自三种熵概念：克劳修斯熵、玻耳兹曼熵和香农熵。在构造出熵的数学函数之后，克劳修斯的进一步研究表明，在孤立系统中熵只增不减。这一表述被称为“熵增加定理”（简称“熵理论”）。而且，“熵增加定理”便被确认为热力学第二定律的数学表述。因而，“熵增加定理”=热力学第二定律，似乎成为不容置疑的“真理”。克劳修斯在提出熵概念之后又提出“宇宙的熵趋于无穷大”，及宇宙最终要走向“热寂”的命题。
 1872年，28岁的奥地利物理学家玻耳兹曼用统计物理方法构造了著名的玻耳兹曼熵表达式：S=KlogD。其中，K为玻耳兹曼常数，D为配容数，又称热力学几率。玻耳兹曼把熵增加定理的微观机制描述为热力学几率的增加。物理学界公认玻耳兹曼第一个发展了克劳修斯的熵的概念，并揭示了“熵”的微观机制。正如普利高津指出：“玻耳兹曼第一个指出熵是分子无序的量度，因此，熵增加定律是一个简单的增加混乱的定律。”他还指出：“玻耳兹曼第一个认识到，熵的不可逆的增加可以是一种分子无序性增长的表达。”玻耳兹曼的这一理论，被称为“玻耳兹曼有序性原理”。
 香农于1948年研究通讯中的数学理论时，构造了一个数学函数：H=-Kni=1!PilogPn。他称此函数为概率集P1……Pn的熵，也称之为“信息（熵）”。在《通讯的数学理论》一书中，香农曾作为一个定理指出：“在有限状态统计源激励下，有限状态变换器的输出也是一个有限态的统计源，它的熵（每单位时间）小于或等于输入统计源的熵。如果变换器是非奇异变换器，它们的熵相等。”在该定理中，所谓非奇异变换器是指无噪声或无干扰的信息传输机构，其信息输入与输出相等。香农的这一理论表明，信息在传输过程中不会增加，但却可能丧失。
 控制论的创始人维纳也看到了这一点，他指出：“信息损失的过程与熵增加的过程十分相似。”“信息可能丧失但不能增加这个事实，就是热力学中的熵恰与信息熵性质相反，因此，维纳认为，“信息量是一个可以看做几率的量的对数的负数，它实际上是负熵”。
 一般系统论创始人贝塔朗菲也持同样的观点。而布里渊则直接指出：“信息意味着负熵”，“信息起着负熵的作用”，“信息是由相应的负熵来规定”，“消耗负熵就是得到信息，而信息可用来增加系统的负熵”。
 除上述理论外，我们还发现两位著名科学大师对熵理论的贡献。一位是薛定谔（1887—1961，量子力学创始人之一），另一位是普利高津。他们都获得了诺贝尔奖。
 1944年薛定谔提出的“有机体就是赖负熵为生”著名命题，近半个世纪以来，在学术界广为流传。他在《生命是什么》一书中提出并论述了著名的“负熵”说。他指出：“生命似乎是有秩序和有规律的行为，它不是完全以它的从有序转向无序的倾向为基础的。”“在我们的食物里，究竟含有什么样的宝贵东西能够使我们免于死亡呢？那是很容易回答的。每一个过程、事件、事变———你叫它什么都可以，一句话，自然界中正在进行着的每一件事，都意味着它在其中进行的那部分世界的熵的增加。因此，一个生命有机体在不断增加它的熵———你或者可以说是在增加正熵———并趋于接近最大值的熵的危险状态，那就是死亡，就是说要活着，惟一的办法就是从环境里不断地汲取负熵，我们马上就会明白负熵是十分积极的东西。有机体就是赖负熵为生的。或者，更确切地说，新陈代谢中的本质的东西，乃是使有机体成功地消除了当它自身活着的时候不得不产生的全部的熵。”这就是著名的薛定谔的负熵说。它被看做是熵经济学的出发点。
 另一位科学大师是普利高津。他把熵理论推向了一个新的高峰。托夫勒在为普利高津的《从混沌到有序》一书所写的前言中指出，普利高津关键论题之一就在于他对熵理论的“惊人的重新解释”。普里高津由于耗散结构理论的建立而获得了1977年诺贝尔化学奖。而其耗散结构理论的一个基本的理论概念或概念工具其实正是克劳修斯所创造的“熵”。普利高津的熵理论包括“最小熵理论”和“超熵产生原理”，其中影响最广的则是其“熵变公式”中的“负熵流说”。其熵变公式为ds=dis+des。即ds（熵的变化）可以分为dis（系统内部的“熵产生”）和des（系统与环境交换的“熵流”）两部分。这一公式的魅力之所在是它即可以解释孤立系统即des=零时的系统状况，又可以解释开放系统的两种可能性。普利高津的“负熵流”导致有序，即“负熵成序”说引入我国后已成为甚为流行的理论，而其在世界学术界的影响也是空前的。
 从熵诞生以来，人们热衷于它，怀疑过它，甚至对它抱否定态度。究竟如何认识这个概念，还尚未有确切、明确的答案。甚至到了1989年，普利高津还专门撰文《熵是什么》，认为“熵是一个很奇怪的概念，不可能给它一个完备个很奇怪的概念，不可能给它一个完备的描述”。但是，熵对诸多学科的影响却是不能否定的，它是后现代的不确定性理论的科学依据。

熵

读音sh·ang(-)，为ang韵目，属ang—iang—uang韵部。
❶物理学中热力学名词。热力学第二定律基本内容是：熵只能增大，决不能减小。

熵shāng

科学技术上泛指某些物质系统状态的一种量度，或者说明其可能出现的程度。

熵shāng

❶ 热力学体系中，不能利用来作功的热能可以用热能的变化量除以温度所得的商来表示，这个商称作熵。
❷ 科技上泛指某些物质系统状态的一种量度或者某些物质系统状态可能出现的程度。1931年《英汉对照百科名汇》：“Entropy，熵。”

熵^*shang

ECD8
❶热力体系中，不能利用来作功的热能可以用热能的变化量除以温度所得的商来表示。这个商叫作熵。
❷科技领域泛指某些物质系统状态的一种量度或某些物质系统状态可能出现的程度。

熵entropy

一个系统中不能用来做功的能量。表示一个系统在能量转化过程中产生无效能，使系统无序性增加的量度。熵与自由能是两个相对的概念，后者是指系统中能做功的能量。当生态系统中的能量从一个营养级流入下一营养级时，一部分能量以热能的形式耗散，导致系统熵值增大和自由能减少。但由于生态系统是一个开放系统，它不断地从外界吸收能量和物质，不断地排除熵，因而可以保持高自由能和低熵，维持系统稳定有序状态。

熵shang

系统状态的函数。系统处于任意确定的状态都具有确定的熵，当系统通过任何过程从一个确定的初态变到另一个确定的终态时，熵的改变量是一定的，与变化过程无关。系统经历任何不可逆过程由初态变到终态时的熵变，可以借助于任何一个连接初、终两状态的可逆过程来计算，即S₂-S₁＝dQ/T，式中1、2表示初态、终态，dQ表示在微小过程中从温度为T的热源吸收的热量。由熵增加原理(见“热力学第二定律”)可知，在孤立系统中进行的过程熵永不减少，dS≥0。可以由熵的变化来判断过程是否可逆及过程进行的方向。而且可以由孤立系处于平衡态时熵值极大，来判断系统是否处于平衡态，如果系统从平衡态有一微小变动，系统熵的变化dS必小于零，因此dS<0是判定孤立系统是否达到平衡的条件。按照统计物理的观点，熵还是系统混乱程度（亦称无序度）的量度，系统越“混乱”，对应的熵越大，平衡态系统中微观粒子运动情况最混乱，对应的熵值极大。

熵

见“物理”中的“熵”。

---

熵

❶热力学系统的状态函数。在任何微分可逆过程中，它的改变等于系统从外界所吸收的热量除以系统的绝对温度。
❷科学技术上泛指某些物质系统状态的一种量度或者某些物质系统可能出现的程度。

熵entropy

见通信一般“熵”。

---

熵entropy

物质系统的无序状态或不确定性的度量。与信息紧密联系。波尔兹曼指出，熵是一个系统失去了的“信息”的度量。一个系统有序程度越高，则熵就越小，所含的信息量就越大；反之无序程度越高，则熵就越大，所含的信息量就越小。根据热力学第二定律可以得出结论，任何孤立系统的熵随时间推移不断增加，开放系统除去与外界相互交流的部分之外，其余部分的熵亦随时间不断增加。熵增原理已被公认为自然界的基本原理。负熵即信息，由于信息量的增加总是导致系统的不确定性的减少，有序的程度的增加，因此，物质系统、社会系统包含的信息量实质上是它的有序化程度的度量。负熵的概念可用于表明信息的属性和运动规律。使用负熵概念，对于进一步揭示信息的本质和运动规律极为重要。信息概念（负熵）反映了物质系统的有序化过程，反映了同热运动方向相反的一切自然运动过程，同熵概念一起，从对立统一的角度揭示了事物发展的规律性。参见“信息”。在交通工程上有两种应用：
❶熵模型，用概率预测交通量的模型之一，通过起讫点调查，推算交通分区间的分布交通量，用以预测远景交通量，因这一模型的一部分与信息论的熵有类似处，故名。
❷中国学者考察混合交通流时，应用熵这一概念，推导出交通熵公式，提供了定性定量地解决混合交通量的新途径。过去统计与分析混合交通量，多用当量换算法，难以确切地描述混合交通的组成性能。

熵

是表明独立物质系统的热力学状态的一个比较抽象的物理量。根据热力学第二定律，热量只能从高温物体传递到低温物体，决定这种传递过程的因素有两方面，一是热量，二是温度，熵就是把热量与温度联系起来表示系统的热力学状态和变化倾向的一个概念。设一个系统中有温度为T₁和T₂两个物体，高温T₁物体把热量△Q传递给温度为T2的低温物体使系统达到平衡，在这种传递过程中△^Q/T1和△Q/T2的差别起了决定作用。这样就把这种热量与温度的比值定义为系统的熵。熵的本质揭示了热力学系统的混乱程度，并从客观上反映了系统的发展趋势。

熵

表示某些物质系统状态的一种量度，或表明这种状态达到的程度。这一概念是由德国物理学家克劳修斯在研究热循环时提出的。熵被视为物质的状态参数，状态一定时，物质的熵值也一定，熵的大小是状态自发实现的可能性的量度。孤立系统达到平衡态时最无序、最混乱，此时熵也处于最大值，因此，孤立系统内实际发生的过程，总是使系统的熵增加。1948年仙农把熵的概念引入信息论，把它作为信息论的基本量，用来度量信息，即熵是用来描写不确定性大小的量。熵值增大，信息的不确定性也越大。熵这一概念还被广泛用于数论、概率论，比利时科学家普利高津说，“我们的兴趣正从‘实体’转变到‘关系’转变到‘信息’，转变到‘时间’上”。因为熵可以为我们描述这些关系和信息的量度。在统计物理学中，熵是关于一个物理系统分子运动状态的物理量，表示分子运动的混乱程度；在信息论中，熵是一个失去了的信息的度量。对孤立系统来说，平衡态的特征是熵最大，体系混乱度最大，无序性最高，组织程度最差，信息量最少，而且一经进入平衡态，便维持这个平衡态，不能飞跃为另一种新质的不同状态。
如果某些宣传工作系统呈现有序化、组织化、复杂化状态，它的量度就是负熵。熵是无序和不确定状态。不确定、无序状态愈来愈趋于确定的有序状态，就是趋于减熵的状态。当宣传工作达到自身维持稳定而又很低的熵的水平上，就是负熵。信息量是任何一个系统确定性、组织性、有序性的量度，信息量的增加即有序程度的增加，也就是熵的减少，那么信息量的急骤增加使某种宣传系统呈现一定方向，出现高度组织化，就是一种负熵状态。

熵

表示某些物质系统状态的一种量度，一般用以表明系统的无序程度和事物的不确定性。熵的概念最初出现在热力学中，用熵的变化来表述热力学自发过程的方向。一个系统若在绝对温度T时的热量增量为dQ，则系统的熵增量为dS≥dQ/T。“=”表示可逆过程，“>”表示不可逆过程。对于绝热过程dQ=0，则有dS≥0，即孤立系统的熵永不减小，熵值达到最大时，系统达到平衡态，过程不再进行。此后，又用熵来描述系统的微观性质，有S=klnW。其中，S表示系统的熵，W表示某一宏观状态对应的微观态数目，k是波尔兹曼常数。系统的无序程度越高，即系统越“混乱”，其对应的微观状态数目越多，因而熵值就越大，从而把熵的概念与系统状态的无序或有序程度联系起来，熵值的大小反映了系统状态无序程度的高低。现在，又把熵的概念引入信息论，用熵来描述和度量事物的不确定性程度，有

式中： S代表事物的不确定性程度，又叫信息熵或信息量，Pi代表事物在n种情况中出现第i种情况的概率。事物的不确定性越大，即Pi越小或n越大，则信息熵S就越大； 在此情形下，若要确切地知道事物的未来情况，则需排除的不确定性就越大，对应所需获取的信息量也就越大。在耗散结构理论、信息论等其他系统理论中，熵是一个重要的概念，因而它被广泛地用于说明各类物理的、生物的、社会的、经济的等各类系统的组织和自组织现象。

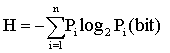
熵shānɡ

 {物} entropy; thermal charge

熵

entropy

熵金文；《説文》所無shāng

[火（意符）+商（聲符）→熵(物理學上指熱能除以溫度所得的商，標誌熱量轉化爲功的程度。)]

^△熵shāng

15画　火部　科学名词。用来表示某些物质系统状态的一种量度，或用来说明其可能出现的程度。
　1.　热力学中表示物质系统热学状态的物理量。
　2.　信息论中的一个基本量。