测量误差celiang wucha

任何测量都有误差。在一个测验中，每个考生的分数均由两部分构成：真实分数(x∞)和误差分数(X_e)。前者是一个理论分数，即表示同一试卷对同一考生测量无数次所得的平均分；后者包括条件误差（如测验工具本身的差异等）和随机误差（如考生作答的心境与临场发挥的情况等）。其表达式为：

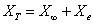
式中 XT——实测分数。
由于X∞一般无法知道，所以X_e也无法知道。为此用下式的测量标准误来估计测量误差：

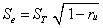
式中 ST——实测的标准差
ru——测验的信度。
故误差分布的标准差，即标准误Se可求。如某次测验中信度为0.91、标准差为10，则可得Se=3。
测量标准误既是测量可靠性(标准误愈小，测量愈可靠)的指标，又是解释测验分数的重要依据。如某次考试中测量标准误为3，若甲生考得80分，则他的真实分数有95%的可能性落在80±6（二个标准误）之间，即74～86分之间。

测量误差

在一切测量中，由于各种因素的影响，测量所得的量值a并不准确地等于被测之量的真值A，二者之差a-A=△a称为测量误差。可分为系统误差和随机误差两大类。由于测量误差是不可避免的，因为无法知道其准确性，人们只能估计在一定的概率下可能达到的误差限，这样估计的误差限称为测量的不确定度。

---

测量误差

见“工程技术”中的“测量误差”。

---

测量误差

误差的一种。按性质可分成两类；1.系统误差。由仪器制造或校正不完善、观测员生理习性、测量时外界条件、仪器检定时的不一致等原因引起。2.随机误差。它的产生取决于观测进行中一系列不可能严格控制的因素(如温度、湿度、空气振动等)的随机扰动。

测量误差

用仪器测量得到的数值与实际值之间的偏差值。按观测误差性质可分为系统误差和偶然误差。系统误差与偶然误差在一定条件下可相互转化。除系统误差和偶然误差外，还有粗差，是由于粗心大意或仪器故障所造成的差错。在测量结果中，不允许粗差存在。

测量误差measurement errors

心理测验理论认为，测量分数会由于样本、被试动机、注意力等各种原因在不同时间和情境中变动，产生偶然误差。引起测量结果变化或不一致的偶然误差，即为测量误差。在实际应用中以测量标准误表示。测量标准误可以理解为多个测验样本分数的标准差，是反映真正分数的分布范围（统计学称离散程度）的指标。测量标准误用途非常广泛，如估计测验分数的范围和置信水平，估计评价信度的指标，比较两个测验分数差异是否显著等。

测量误差

measuring error

测量误差measure error

指实测值与真值之差。实测值是实际测量某种事物或现象时所获得的测定值，也称实测分数(X)。真值是被测量的事物或现象的真实规模(如实际的长短、轻重、大小等)的取值，也称真分数(T)。两者之差即称为测量误差或误差分数(E)。因与测量目的无关的因素引起致使测量结果不准确或不一致。分随机误差和系统误差两类。前者受各种偶然因素影响，使多次测量结果不一致，它对测量的信度、效度都有影响；后者又称恒定误差，由稳定因素引起的方向和大小有规律可循的误差，只影响测量的效度，不影响信度。

测量误差measurement error

由与测量目的无关的因素引起，使测量结果不准确或不一致的效应。分随机误差和系统误差两类。前者是受各种偶然因素影响，使多次测量结果不一致；后者又称恒定误差，是由稳定因素引起的方向和大小有规律可循的误差。系统误差只影响测量的效度，不影响信度；随机误差对信度、效度都有影响。

测量误差measurement error

即“误差”。

测量误差

某量真值与其观测值之差。由仪器不够完善、观测者的感觉器官鉴别能力和技术水平、大气折光、气温变化等因素引起。按性质可分为： (1) 系统误差，其正负和大小带有规律性，使观测值偏大或偏小。(2) 随机误差，其正负和大小表现出随机性，总体上服从一定的统计规律。测量中随机误差服从正态分布。(3) 粗差，是绝对值超出随机误差的限值的一种误差和错误。