毕达哥拉斯定理bidagelasi dingli

参见“勾股定理”.

毕达哥拉斯定理

这个定理说明，在任何直角三角形中，斜边上的正方形面积等于另两边上的正方形面积之和：r²＝ x²+ y²，欧氏平面几何中这个极为重要的定理，是以公元前六世纪希腊哲学家和数学家毕达哥拉斯命名的，它已有100余种证明方法，其中一个证明是由比较图1中正方形的面积而得到的。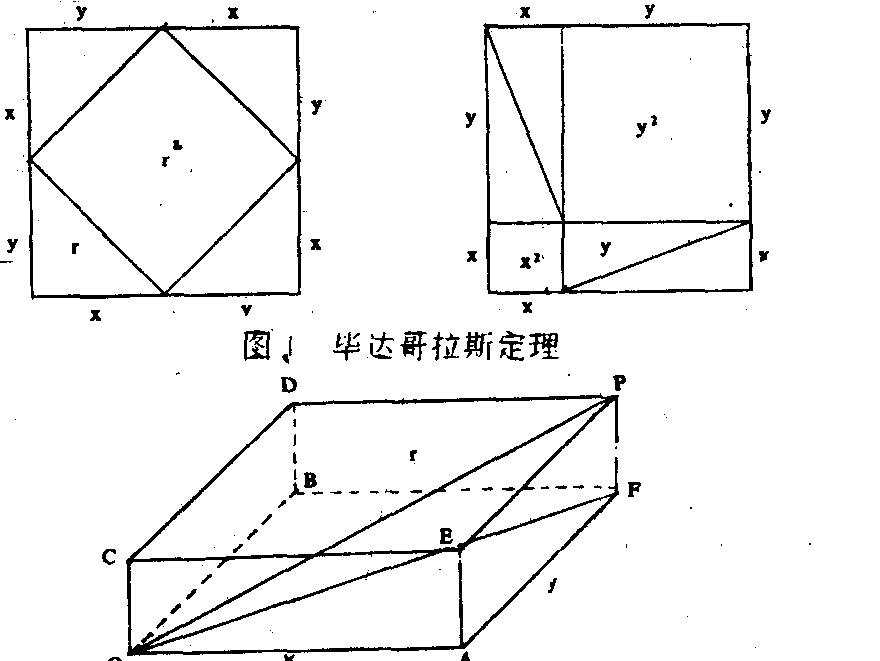
图2 三维毕达哥拉斯定理三维毕达哥拉斯定理可叙述为(见图2):长方体的对角线的平方等于交于一顶点的三边的平方之和：r^2=x2+y2+z2。毕达哥拉斯定理已知一些数的平方等于两个或三个数的平方之和，例如3²+4²＝5²,1²+4²+8²＝9²。满足x²+y²＝r2的任何三整数组见图2:长方体的对角线的平方等于交于一顶点的三边的平方之和：r^2=x2+y2+z2。
毕达哥拉斯定理已知一些数的平方等于两个或三个数的平方之和，例如3²+4²＝5²,1²+4²+8²＝9²。满足x²+y²＝r2的任何三整数组(x,y,r)称毕达哥拉斯三数组，四数组依此类推，在三数组(a²-b²,2ab,a2+b²)中，用和为奇数且无公因子的整数代替字母a和b，可得x,y,r无公因子且x为奇数的所有毕达哥拉斯三数组。