正交设计orthogonal design

用正交表安排的部分实施多因素试验。任何两列数据只要具备以下两个条件，即称为正交。式(1)称为正交条件

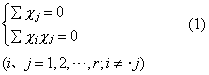
正交表用有限域理论构造而成，表中任何两列数据都符合正交条件。应用最多的是L(tq)类型正交表。L表示正交表，t为因素的水平数，t限制为素数或素数幂。u为基本列数，可以是任何正整数。水平数和基本列数决定后，t就是处理组合数。q为正交表中的列数，q=t-1/t-1。常用的正交表为L₈(2⁷)表。表中1,2为两个试验水平代号。第1列定列名为a，将8个处理二等份，分别记作1水平和2水平，称为二分列。第2列记列名为b，是第1列的二分列。第4列记列名为c，是第2列的二分列。每个二分列即为一个基本列。每个基本列后跟有前方各列的交互作用列。每个基本列到下个基本列之间的列称为群。正交表上的水平代号经一定形式数据变换后即符合式(1)。正交表具有两个特点：❶搭配均衡：表1中每列都有相等数目的1、2水平，任两列共有四种水平组合(1,1)、(1,2)、(2,1)、(2,2)。这种组合称为有序对。在8个处理组合中每种组合各出现两次，这就是搭配均衡。
❷整齐可比：表1中的3个基本列上依次安排氮磷钾3种肥料因素，1水平代表不施肥。第1列上处理1～4均为不施氮，这4个处理在第2～7列上都是1,2水平各两次。第1列上处理5～8为施氮肥，在第2～7列上也是1,2水平各两次。第1列上1水平之和与2水平之和的差数就是施氮肥的效应。这时第2～7列上1,2水平都是均衡的，这就是正交表的整齐可比性质。基本列外的其他列都是交互作用列，已制成相应正交表的交互作用表——L₈(2⁷)的交互作用表如下：

表2 L₈(2⁷)两列间的交互列

1	2	3	4	5	6	7	列号
(1)	3	2	5	4	7	6	1
	(2)	1	6	7	4	5	2
		(3)	7	6	5	4	3
			(4)	1	2	3	4
				(5)	3	2	5
					(6)	1	6
						(7)	7

从表2可以查出任二列的交互作用效应的位置。交互作用表是设计正交试验的重要工具。不少正交表已从交互作用表查出主效应不与交互作用混杂的设计表(简称表头设计表见表3)。当正交表为不完全实施方案时，必有一部分效应重叠出现于同一列中。这一列两水平的差数是混杂的，用正交设计试验对各因素所起作用做结论时需十分谨慎，以免作出错误的结论。但正交设计不同因素水平间搭配均衡，只要水平设置较为合理，将不会遗漏试验数据较好的处理组合，试验结果将会是很好的。从中选出最佳的处理组合，以此为基础进一步设计可分析出交互作用效应的第二轮试验，可以加快研究进度。这是正交设计的突出优点，也是快速找出肥料配方的好方法。

表1 L₈(2⁷)

列号 试验号	1	2	3	4	5	6	7
1	1	1	1	1	1	1	1
2	1	1	1	2	2	2	2
3	1	2	2	1	1	2	2
4	1	2	2	2	2	1	1
5	2	1	2	1	2	1	2
6	2	1	2	2	1	2	1
7	2	2	1	1	2	2	1
8	2	2	1	2	1	1	2

表3 L₈(2⁷)表头设计

列号 因素数	1	2	3	4	5	6	7	实施
3	A	B	AB	C	AC	BC		1
			AB		AC	BC
4	A	B		C			D
			CD		BD	AD		1/2

二水平多因素正交试验 因素数目根据专业研究需要确定以后，找出适当正交表的表头设计表，将各因素及水平代入正交表中即得正交试验的各处理组合。线性数学模型根据表头设计中未混杂的各因素主效应及交互效应列入，被混杂的各列都并入随机误差中

y＝μ+A_i+B_j+…+(AB)_ij+…+(2)-
(α=1,2，…，t;i,j，…=1,2，…)

式(2)中 α为处理组合数，i,j为每个因素的水平数。A_i、B_j、…、(AB)_ij…为各个因素及交互作用，ε为各处理组合的随机误差。
根据式(2)进行平方和及自由度分解后做方差分析。若正交设计已设置重复，则线性数学模型中还需加入组区效应项。常用的二水平正交表有L₄(2³)、L₈(2⁷)、L₁₆(2¹⁵)、L₃₂(2³¹)、L₆₄(2⁶³)等。
三水平正交试验 常用的三水平正交表有L₉(3⁴)、L₂₇(3¹³)两种，偶而也用L₈₁(3⁴⁰)。它们的基本参数t为3,μ为2、3及4，列数q=t-1/t-1分别为4、13及40。L₂₇(3¹³)正交表如下：

表4 L₂₇(3¹³)

L₂₇(3¹³)正交表的交互作用表如下：

表5 L₂₇(3¹³)二列间的交互作用

列号	1	2	3	4	5	6	7	8	9	10	11	12	13
1	(1)	3 4	2 4	2 3	6 7	5 7	5 6	9 10	8 10	8 9	12 13	11 13	11 12
2		(2)	1 4	1 3	8 11	9 12	10 13	5 11	6 12	7 13	5 8	6 9	7 10
3			(3)	1 2	9 13	10 11	8 12	7 12	5 13	6 11	6 10	7 8	5 9
4				(4)	10 12	8 13	9 11	6 13	7 11	5 12	7 9	5 10	6 8
5					(5)	1 7	1 6	2 11	3 13	4 12	2 8	4 10	3 9
6						(6)	4 5	4 13	2 12	3 11	3 10	2 9	4 8

（续） 列号 1 2 3 4 5 6 7 8 9 10 11 12 13 7 　 (7) 3 12 4 11 2 13 4 9 3 8 2 10 8 　 　 (8) 1 10 1 9 2 5 3 7 4 6 9 　 　 　 (9) 1 8 4 7 2 6 3 5 10 　 　 　 　 (10) 3 6 4 5 2 7 11 　 　 　 　 　 (11) 1 13 1 12 12 　 　 　 　 　 　 (12) 1 11

L₂₇(3¹³)为主效应不与交互作用效应混杂表只有两种表头设计(表6)。

表6 L2₇(3¹³)的表头设计

列号 因素数	1	2	3	4	5	6	7
3	A	B	AB	A2B	C	AC	A2C
4	A	B	AB C2D	A2B	C	AC B2D	A2C
列号 因素数	8	9	10	11	12	13	实施
3	BC			B2C			1
1	BC A2D	D	AD	B2C	BD	CD	1/3

如有5～7个因素，通常的做法是在因素为3的表头设计中的9、10、12、13四个空列中填入其他因素，得到部分实施程度分别为1/9、1/27、1/81实施的试验方案。线性数学模型与式(2)相间，但i,j，…=1,2,3。
正交拉丁方试验 当μ=2时L₂₁＝(t¹⁺¹)系列的正交表称为正交拉丁方系。常用的有L₉(3⁴)、L₁₆(4⁵)、L₂₅(5⁶)，这些正交拉丁方系也称为3×3、4×4、5×5正交拉丁方。不存在6×6的正交拉丁方。7×7、8×8、9×9、10×10、12×12的正交拉丁方也可从书籍中查到。当试验因素只有两个时是完全实施方案。因素数多于两个时正交拉丁方试验都是高度混杂的。多数试验者是着眼于从多个水平的均衡搭配中找出较好的处理组合，直接用于生产或作为进一步试验的基础，因此并不都进行统计分析，即使进行统计分析，各项效应中也混杂有其他效应，做结论时应谨慎。
拟水平法 正交表有严密的固定形式，但试验者所需的各因素的水平数不一定与正交表中完全一致。拟水平法是将较少的试验水平安排到水平数较多的正交表上的试验设计技术。具体办法是虚拟一个原已确定的水平，使这个虚拟水平的重复数增加一倍。线性数学模型与式(2)相似，但拟水平因素的自由度应减1。
并列法 试验所需水平数常多于常用正交表上的水平数。并列法可将正交表上两个或三个列合并为一个水平数成倍增加的新列，从而构造出水平数更多的或水平数不等的混合型正交表的技术。线性数学模型与式(2)相同。
拟因子法 将二水平正交表通过并列改造为三水平正交表的方法。与三水平正交表相比，拟因子法制成的新表可使更多的交互作用效应不被混杂，但这种新表丧失了正交性，不同水平互比时，需将上半表与下半表的各水平平均值进行校正。拟因子法优点较多，但技术要求较高。线性数学模型与式(2)相同。
裂区正交试验 用正交表安排的正交裂区试验中常与拟因子法合并应用，例如需研究A、B、C、D四种肥料的主效应与全部两因素交互作用效应，每个因素各又有三个水平，并要求C、D两种肥料因素有较高的精度要求。这种试验采用完全实施方案的裂区试验有81个处理组合(3⁴＝81)，如用拟因子法将正交表L₃₂(2³¹)改造为三水平表，用32个处理组合即可达到目的。安排试验时需遵循以下规则：❶低级因素尽量安排在低级群中；
❷同级因素尽量安排在同级群中，不同级因素安排在不同群中；
❸不同群的两列间交互作用必在其较高群中；
❹同一群中的两列间交互作用必在其前面群中；
❺第1列不可排因素，令其赋闲。其线性数学模型为：

y＝μ+A_j+B_k+(AB)_jk+(CD)
+(ε₁)_jk+G_l+D+(AC)_jl (3)
+(BC)+(AD)+(ε₂)

用一次误差ε₁检验一级因素及交互作用，二级误差ε₂检验二级因子。进行多重比较时因采用了拟因子法，故水平平均值亦需作校正。
并表法 将一张规模较大的正交表分解为两张或两张以上较小的正交表，然后根据不同研究目的采取适当的应用方式的试验方法。应用方式有多种，例如将L₈₁(3⁴⁰)正交表的81个处理组合改造为9张L₉(3⁴)正交表，合起来就是一张L₈₁(3⁴⁰)，分开来是9张不同处理的L₉(3⁴)正交表。在9个地点进行试验，再集中到一起按L₈₁(3⁴⁰)正交表整理试验结果，优点是可以使每个地点的试验规模不大，便于管理，同时也可探索全部81个处理组合的总的规律。不足是这种方式在因素间是高度混杂的。另一种是有些因素的水平数较多，这些水平因性质有一定差异而需分组比较，另一些因素的水平全部一样。如分两个试验则将损失一部分信息，这耐可将一张大正交表分解为两张较小的正交表，在同一地点分两个小试验同时试验，再集中至一起统计分析。由于总自由度的增加，改善了统计性质，提高了分析精度。这类试验的线性数学模型随应用方式而有较大区别，应根据具体试验内容进行统计分析。

正交设计zheng jiao sheji

用一套规格化的表格即正交表来安排的实验设计。在此种设计中，每个因子在各个水平上出现的次数相等， 任意两个因子在各种水平搭配上出现的次数相等，即实验具有正交性。由于设计的正交性意味着平衡、可分离，所以实验结果的统计分析较简单。数据分析可采用直观分析比较法，但大多使用方差分析法。在需要建立数学模型时，也可采用回归分析。

正交设计orthogonal design

是多因素试验的一种设计方法。它利用一种规格化的正交表，将多因素进行合理安排，在既保证最小的试验次数，又保证得出全面结论的前提下，将各因素的各水平均匀搭配，使任何两个因素间的不同水平各遇到相同的次数。采用正交设计不仅可分清各个因素的作用，并可进一步分析主要的交互影响。