极坐标系jizuobiaoxi

在平面内取一个定点O，从O引一条射线OX，选定一个单位长度以及计算角度的正方向（通常取逆时针方向为正方向），这样就建立了一个极坐标系（如图）.O点叫做极点，射线OX叫做极轴.
设M点是平面内任意一点，用p表示线段OM的长度，θ表示射线OX到OM的角度，那么p叫做M点的极径，θ叫做M点的极角，有序数对(p,θ)叫做M点的极坐标.

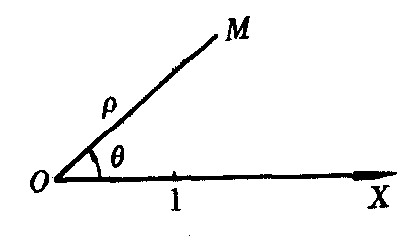
中学解析几何教材中规定，不作特殊说明时，认为极径p≥0.但是，在某些必要情况下，也允许ρ取负值.当ρ<0时，点M(ρ,θ)的位置按下列规则确定：作射线OM′，使∠XOM′=θ，在OM′的反向延长线上取一点M，使|OM|=-ρ，则M就是坐标为(ρ,θ)的点.
总之，平面上点的极坐标(ρ,θ)有狭义和广义之别：
当0≤ρ<+∞,0≤θ<2π时，把(ρ,θ)叫做点M的狭义极坐标.这时，除极点外，平面上的点与有序数对(ρ,θ) (ρ≠0)是一一对应.
当-∞<ρ<+∞,-∞<θ<+∞时，把(ρ,θ)叫做点M的广义极坐标.在广义极坐标下，平面上的点与它的坐标是一多对应.
定理1 极点的坐标(0,θ),(θ∈R)有无限多个.
定理2 非极点M的坐标也有无限多个.如果(ρ₀,θ₀)是它的一个坐标，那么(ρ₀,θ₀+2kπ)及(-ρ₀,θ₀+ (2k+1)π)(k∈Z)都是点M的坐标.此二式可统一地写成( (-1)^kρ₀,θ₀+kπ) (k∈Z)的形式.反之，M点的任何坐标都能写成如上两种形式之一，即如果(ρ,θ)是M点的一个坐标，那么必存在一个整数k0，使ρ=(-1)^k0ρ₀且θ=θ₀+k0π.