旋转体的体积
旋转体的体积xuan zhuanti de tiji
若一连续曲线y=f (x) 的弧AB (假定它并不与X轴相交,如图1)与直线x=a,x=b及X轴围成的平面图形绕X轴旋转一周,产生了一个旋转体,则这个旋转体的体积
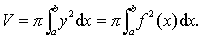
若连续曲线x=ψ (y)的弧CD(假定它并不与Y轴相交,如图2)与直线y=c,y=d及Y轴围成的平面图形绕Y轴旋转一周,产生了一个旋转体,则这个旋转体的体积
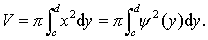
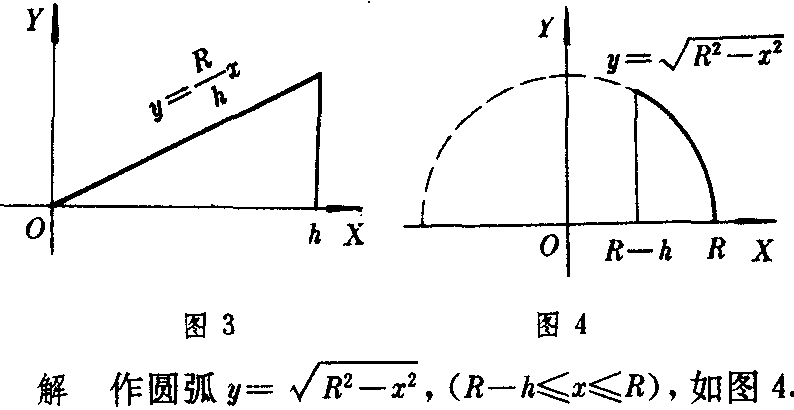
图1
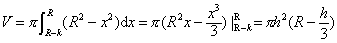
图2
利用旋转体体积公式容易推出圆柱、圆锥、圆台、球缺的体积公式.
例1 求高为h,底面圆半径为R的圆锥的体积V.
解 作线段y=R/h x,(0≤z≤h),如图3.该线段与直线x=h及X轴围成的平面图形绕X轴旋转一周产生的旋转体就是已知的圆锥.由旋转体体积公式,有
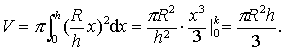
例2 已知球的半径为R,球缺的高为h (h
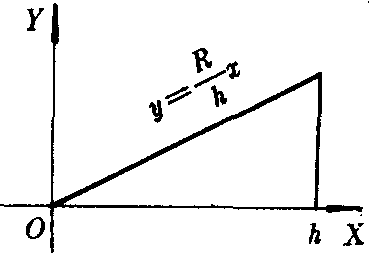
图3
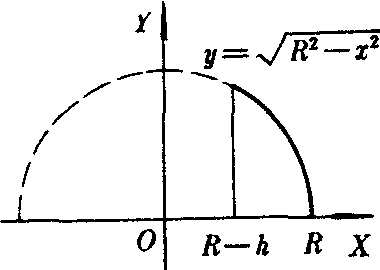
图4
解 作圆弧
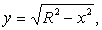 (R-h≤x≤R),如图4.该圆弧与直线X=R-h及X轴围成的平面图形绕X轴旋转一周产生的旋转体就是已知的球缺. 由旋转体体积公式,它的体积
(R-h≤x≤R),如图4.该圆弧与直线X=R-h及X轴围成的平面图形绕X轴旋转一周产生的旋转体就是已知的球缺. 由旋转体体积公式,它的体积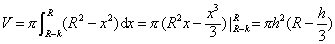
☚ 平面图形的面积 平面曲线的弧长 ☛
- 固定费用预算是什么意思
- 固定资产是什么意思
- 固定资产与流动资产是什么意思
- 固定资产中小修理是什么意思
- 固定资产交付使用率是什么意思
- 固定资产产值率是什么意思
- 固定资产价值是什么意思
- 固定资产估价是什么意思
- 固定资产余值是什么意思
- 固定资产使用年限是什么意思
- 固定资产依法处分权是什么意思
- 固定资产修理是什么意思
- 固定资产内涵扩大再生产是什么意思
- 固定资产再投资是什么意思
- 固定资产再生产是什么意思
- 固定资产再生产理论是什么意思
- 固定资产再生产结构是什么意思
- 固定资产再生产计划是什么意思
- 固定资产净值是什么意思
- 固定资产净值率是什么意思
- 固定资产净投资是什么意思
- 固定资产净残值是什么意思
- 固定资产减值是什么意思
- 固定资产减值准备是什么意思
- 固定资产分类是什么意思
- 固定资产利用分析是什么意思
- 固定资产利用指标是什么意思
- 固定资产利用效果分析是什么意思
- 固定资产利用率是什么意思
- 固定资产利用率指标是什么意思
- 固定资产利稅率是什么意思
- 固定资产利税率是什么意思
- 固定资产动用系数是什么意思
- 固定资产单项折旧率是什么意思
- 固定资产原价是什么意思
- 固定资产原值是什么意思
- 固定资产原始价值是什么意思
- 固定资产变价收人是什么意思
- 固定资产变价收入是什么意思
- 固定资产变动表是什么意思
- 固定资产变卖是什么意思
- 固定资产变卖收入是什么意思
- 固定资产周转率是什么意思
- 固定资产和流动基金增减表是什么意思
- 固定资产回收率是什么意思
- 固定资产增值是什么意思
- 固定资产增加是什么意思
- 固定资产增长率是什么意思
- 固定资产外延扩大再生产是什么意思
- 固定资产大修理是什么意思
- 固定资产大修理基金提存率是什么意思
- 固定资产定额是什么意思
- 固定资产审计是什么意思
- 固定资产帐是什么意思
- 固定资产平衡表是什么意思
- 固定资产废弃系数是什么意思
- 固定资产形成是什么意思
- 固定资产恢复是什么意思
- 固定资产扩大再生产是什么意思
- 固定资产扩建是什么意思