整数加法Zhengshu jiafa

常用的自然数理论有基数理论与序数理论两种， 自然数的加法运算也可以有两种相应的定义。
用基数理论来定义：如果A和B是两个不含有公共元素的有限集合，它们的基数分别是a和b，集合A和B的并集为C, 那么集合C的基数就叫做a与b的和。记作a+b=c。
用序数理论来定义：如果a和b都是自然数，在自然数列中的数a之后再数出数b来恰好对应自然数列中的数C, 那么数C就叫做a与b的和， 记作a+b=c。
在上述两种定义中， a与b都叫做加数， 符号“+” 叫做加号， 读作 “a加b等于c”。
当加数为零时， 补充定义： 0+a=a, a+0=a, 0+0=0。
无论是从基数理论还是从序数理论出发定义加法，求两个数的和都可以归结为数数：从1开始，先数出a来， 接着再数出b来， 所得的结果就是a与b的和。由于数数总能进行，并且所得的结果是唯一的，所以对于任何非负整数a和b总可以得到唯一确定的非负整数c作为a与b的和，也就是说，非负整数的加法运算总是能施行的。
非负整数的加法具有下列性质： 加法的和不小于任意一个加数， 即a+b≥a, a+b≥b。
加法运算律
❶加法交换律：两个数相加，交换加数的位置， 它们的和不变， 即a+b=b+a。
❷加法结合律：三个数相加，先把前两个数相加，再加上第三个数；或者先把后两个数相加再加上第一个数，它们的和不变， 即 (a+b) +c=a+ (b+c)。这两个运算律成立， 是由于计数的结果与计数的顺序无关。
加法的计算法则
❶一位数的加法： 两个一位数相加，可以直接用数数的方法求出和。通常把两个一位数相加的结果编成加法表。
❷多位数的加法：相同数位上的数相加；哪一位上的数相加满十，再向前一位进
多位数加多位数， 可以先把两个多位数写成不同计数单位的和的形式， 再根据加法的运算律和一位数加法法则， 分别把相同计数单位的数相加。例如：

通常将上述计算过程， 写成竖式， 即

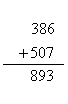
多位数加法竖式的计算法则是：数位对齐，从个位加起， 满十进一。