拉丁方试验

用r个拉丁字母排成r行r列的方阵，使每行、每列中每个字母都只出现一次，这样的方阵叫r阶拉丁方或r×r拉丁方。按拉丁方的字母、行和列安排处理及影响因素的试验称为拉丁方试验。如采用5×5拉丁方(r=5)安排五个受试者在五个不同日期穿五种防护服测量脉搏数(次/分)的试验中：日期1，受试者甲穿D种防护服，受试者乙穿B种，丙穿A种，……； 日期5，受试者甲穿E种，……，戊穿D种。这样，穿每种防护服的脉搏数，都是从五个人在不同的五天中测得的，受气候条件和受试者个体差异的影响相同。因此，能更精确地比较五种防护服对脉搏的影响。

试验日期	受 试 者
	甲	乙	丙	丁	戊
1 2 3 4 5	D B C A E	B E A D C	A D E C B	E C D B A	C A B E D

设计 要求：
❶必须是三个因素的试验，且三个因素的水平数相等；
❷行间、列间、处理间均无交互作用；
❸各行、列、处理的方差齐。方法：
(1)根据处理数选定拉丁方(参见有关统计书，列有各种基本型式的拉丁方)。
(2)将拉丁方随机化。使用基本型拉丁方时要加以随机化，用列的重排和行的重排来实现，但交换或移动时必须整列（或行）进行，不能将列或行拆散。例如5×5拉丁方的随机化：

(3)规定行、列、字母所代表的因素和水平。如前例，行为试验日期1,2，…，5；列为受试者甲，乙，…，戊；字母为防护服种类A,B，…，E；各为5个水平。
分析 由于各因素、水平是有规律的安排，就可用方差分析把原来包含在试验误差中的行间和列间的变异分离出来，既减少了试验误差，提高了试验的效率，又可作行间、列间均数的比较。计算步骤如下：
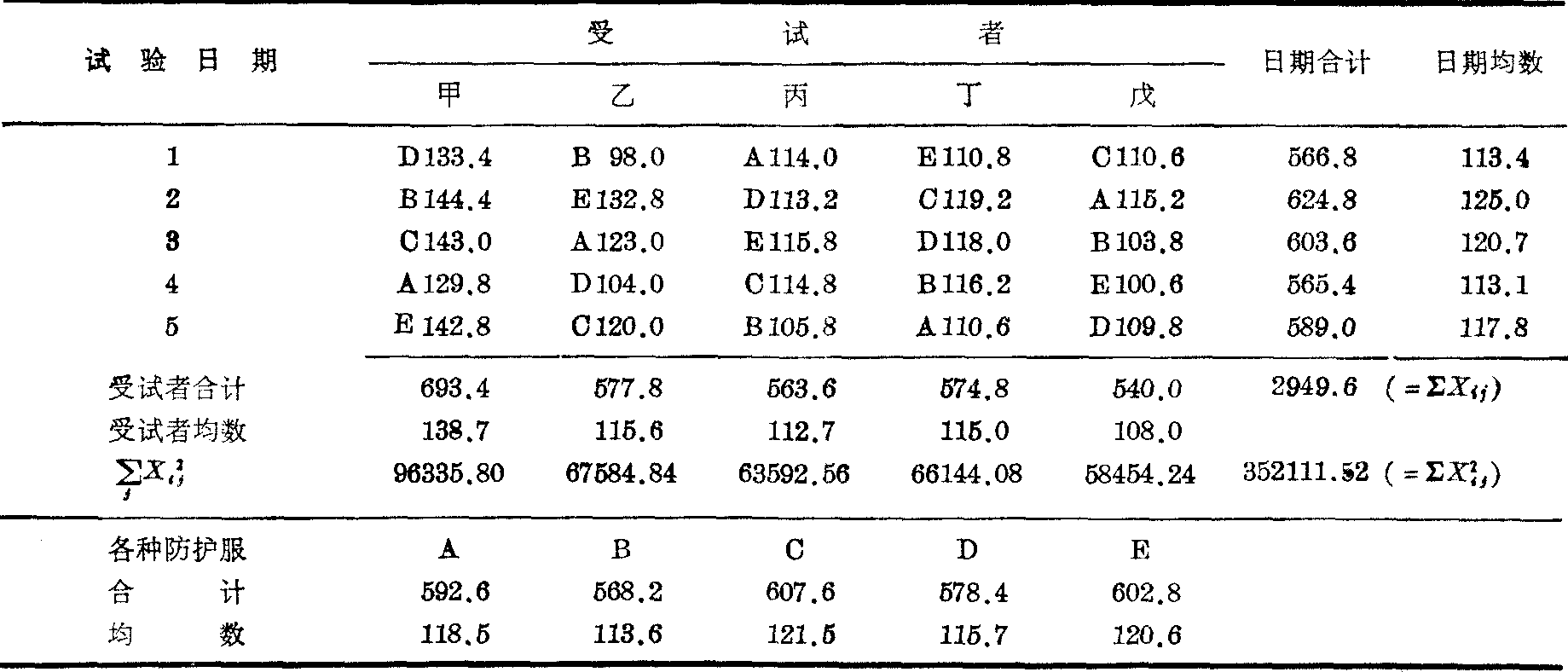
(1)列出试验结果，进行初步计算如表2。各处理(防护服A,B，…，E)的合计及均数，是将数据中该处理的全部观察值相加并平均求得。如处理A的合计=114.0+115.2+123.0+129.8+110.6=592.6，均数=592.6/5=118.5。
(2)按表1公式计算离均差平方和SS、自由度v、均方MS与F值。

表1 方差分析用公式

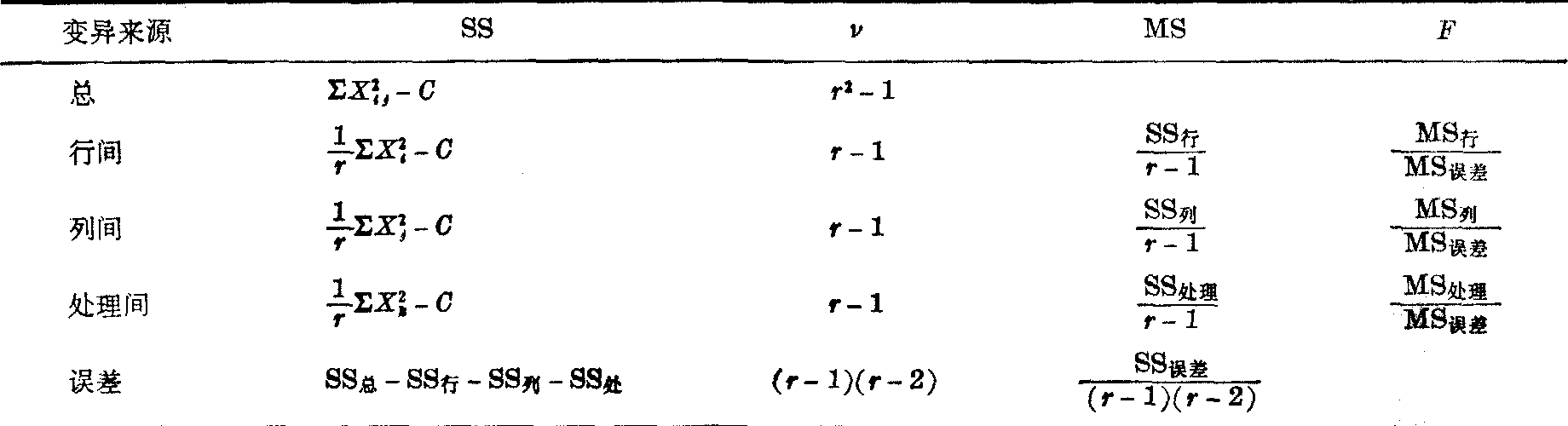
表1中X_i为第i行小计，X_j为第j列小计，X_k为第k种处理小计，校正数C=(∑X_ij)²/r²,X_ij为第i行第j列观察值，r为拉丁方的阶，即行数、列数或处理数。
(3) 查F界值表得P值，按所取检验水准作出推断结论。
(4)若检验结果均数间有差别，需要时作均数的两两比较(见条目“多个样本均数间两两比较”)。
例1 为比较五种防护服对脉搏数的影响，考虑到：
❶根据处理数为5 （防护服种数）决定用5个受试者，在5个不同日期进行试验；
❷受试者的脉搏数互不影响，各受试日期对脉搏数无影响，各种防护服对脉搏数的影响无持续的后效应，因此无交互作用；
❸假定各行、列、处理脉搏数的方差齐，故选用5×5拉丁方经随机化后安排实验，得结果如表2上半部，试进行方差分析。

表2 穿五种防护服测得的脉搏数(次/分)

日期间：
H₀: 各日期脉搏均数相等，
H₁: 各日期脉搏均数不等或不全相等。受试者间：
H₀: 各受试者脉搏均数相等，
H₁: 各受试者脉搏均数不等或不全相等。防护服间：
H₀: 穿各种防护服脉搏均数相等，
H₁: 穿各种防护服脉搏均数不等或不全相等。均取α=0.05。
+(602.8)^x]-348005.61=218.02,
SS误差=4105.91-508.07-2853.67-218.02=526.15。

表3 方差分析

变异来源	SS	v	MS	F	P
总	4105.91	24
日期间 受试者间 防护服间 误 差	508.07 2853.67 218.02 526.15	4 4 4 12	127.02 713.42 54.51 43.85	2.90 16.27 1.24	>0.05 <0.01 >0.05

查F界值表得P值，见表3。按α=0.05水准日期间和防护服间均不拒绝H0，受试者间拒绝H0，接受H1。即各试验日期，穿各种防护服，受试者的脉搏均数看不出差别，但各受试者间脉搏有差别。从表2受试者均数行中可看出，受试者甲的脉搏较快。必要时可进行均数间两两比较。
缺项估计 拉丁方试验的特点是各行、各列、各处理的观察值个数相等。当实验中遇到意外情况，如一个动物因其他原因死亡、试管打破或发现明显的记录错误等，致数据漏失时，可以对所缺数据进行估计。但缺项估计的目的只是为了资料分析能顺利进行，所估数据不对实验提供任何信息。
只缺一个数据时，用式(1)估计缺项Xeò 补入Xe后，按无缺项的拉丁方作方差分析。但进行方差分析时要从SS处理中减去偏大值K(按式(2)计算)，并将总变异和误差的自由度各减1。

式中r为拉丁方的阶，R为有缺项行内各观察值之和，C为有缺项列内各观察值之和 （非方差分析中的校正数）,T为有缺项处理内各观察值之和，G为观察值总和（不包括估计值）。
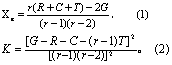
若需将有漏失数据的处理均数和其他处理的均数进行比较时，两均数之差的标准误S1～2按式(3)计算。

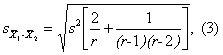
式中S²是补入缺项后算得的误差均方。
例2 假定表2中受试者丙，日期4穿C种防护服的数据漏失，试作缺项估计后，比较五种防护服对脉搏的影响。
r=5,R=450.6,C=448.8,T=492.8,G=2834.8，代入式(1)、式(2):

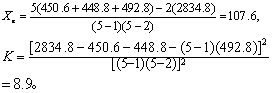
将表2中的缺项(原为114.8)补入107.6后，仍按例1步骤计算SS总、SS日期、SS受试、SS误差，但SS防护须减K，即

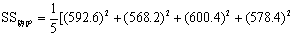
+(602.8)²]-(2942.4)²/25-8.9=166.50,
结果见表4。

表4 方差分析

变异来源	SS	v	MS	F	P
总	4201.53	23
日期间 受试者间 防护服间 误 差	586.99 2937.77 166.50 510.27	4 4 4 11	146.75 734.44 41.63 46.39	3.16 15.83 0.90	>0.05 <0.01 >0.05

所得结论和原结论同。
不完全拉丁方 又称Youden方。当客观条件限制不能用拉丁方试验时，可用拉丁方的一部分来安排试验，称为不完全拉丁方试验。或虽用了拉丁方试验，但由于漏失数据较多，又无法补救时，可根据情况作不完全拉丁方资料处理。计算步骤如下：
(1)计算现有数据各行、列、处理的合计，如表5。
(2)计算校正数C及SS行、SS列、SS总，公式见条目“配伍组试验”。
(3) 以各列（或行）均数估计该列（或行）所缺数据，并与相应处理的合计相加，作为各处理合计的估计值。如表5中第一列均数为55.4/3=18.5，将18.5补入该列第一行，其处理为D，与D处理原合计数相加得18.5+83.1=101.6，即D处理合计的估计值，余类推。为了便于计算，将此式所有数值乘(n-1)得Ti。此例n为4，因此TD的计算变为TD=55.4+83.1×3=304.7，余类推。将各Ti代入式(4)计算SS处理。

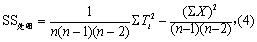
式中∑X为观察值的合计（不包括估计值）。
(4)计算SS误差，按式(5),
SS误差=SS总-SS行-SS列-SS处理。 (5)(5) 列出方差分析表，查F界值表得P值，按所取检验水准作出推断。
例3 表5资料缺第一行，试比较家兔注射不同剂量胰岛素后，血糖降低百分比间有无差别。

表5 家兔注射胰岛素后血糖降低百分比

注射日期		家 兔 编 号				日期合计
月	日	1	2	3	4
6	30	D	C	B	A
7 7 8	9 28 6	B 26.2 C-4.0 A 33.2	A31.8 D14.0 B16.5	D28.9 A27.5 C21.2	C18.7 B25.6 D40.2	105.6 63.1 111.1
家兔合计		55.4	62.3	77.6	84.5	279.8
剂量合计		A:92.5	B:68.3	C:35.9	D:83.1

H₀: 各剂量组血糖降低百分比的各均数相等，
H₁: 各剂量组血糖降低百分比的各均数不等或不全相等。
α=0.05。

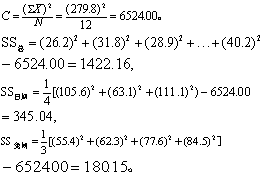
	D	C	B	A
(1)各列合计 (2)原剂量合计×3 Ti=(1)+(2)	55.4 249.3 304.7	62.3 107.7 170.0	77.6 204.9 282.5	84.5 277.5 362.0

按式(4)及式(5):

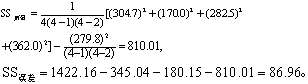
表6 方 差 分 析

变异来源	SS	v	MS	F	P
总	1422.16	11
日期间 兔 间 剂量间 误 差	345.04 180.15 810.01 86.96	2 3 3 3	172.52 60.05 270.00 28.99	5.95 2.07 9.31	>0.05 >0.05 <0.05

查F界值表得P值，见表6，各剂量间按α=0.05水准拒绝H₀，接受H₁，可以认为家兔注射不同剂量胰岛素后血糖降低百分比有差别，C剂量组血糖降低百分比小。