抽样分布sampling distribution

样本统计量的概率分布。它是样本推断总体的理论基础。按随机抽样方式从总体抽取一定容量的所有可能的样本，样本统计量如平均数，方差S²,t值等等将形成特定的概率分布。农业化学研究中常用的抽样分布有如下几种：
样本平均数的分布 如果从平均数为μ，方差为σ2的总体X中随机抽取容量为n的样本：x₁,x₂，…，x_n，则样本平均数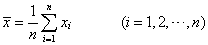
其分布性质为：❶μ_＝μ (μ_为样本平均数分布的数学期望);
❷σ_²＝σ²/n)(σ_²为样本平均数分布的方差);
❸如果x～N(μ,σ²)，则～N(μ,σ²/n);
❹如果母总体X具有平均数μ，方差σ²，但分布不呈正态或分布形式未知，则随样本容量n的增大，样本平均数的分布渐趋于正态分布。
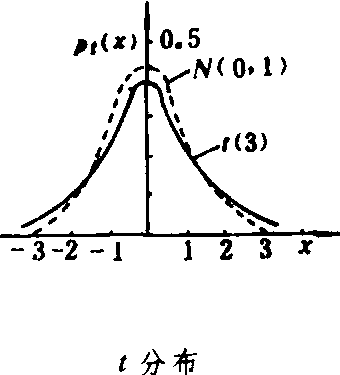
样本平均数差数的分布 如果从平均数为μ₁，方差为σ₁²的总体X₁中随机抽取容量为n₁的所有可能样

式中 π为3.14159…，v为自由度。t分布是随自由度v不同而变化的一组曲线，自由度较小时t分布曲线较标准正态分布曲线低矮离散，v愈大愈接近标准正态曲线；v→∞时，t分布逼近标准正态分布（见图）。t分布的平均数为0。曲线以t=0为中心左右对称，t定义域(-∞,∞)。实际上统计量t已被广义化，不一定限于上述定义，任何统计量只要它的密度函数符合p(t)要求都可以看作t分布。

χ²分布 从一个平均数μ和方差σ²已知的正态总体X中随机抽取容量为n的样本，x₁,x₂，…，x_n，则统计量χ²定义为

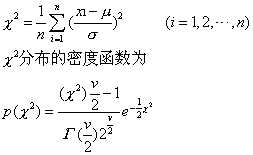
式中 v为自由度等于n。如果总体平均数μ未知，则
线倾斜，且随自由度减小倾斜度加剧。X²的定义域为(0,∞)。实际上任一统计量只要其密度函数与p(X²)相符都是具有X²分布的统计量。

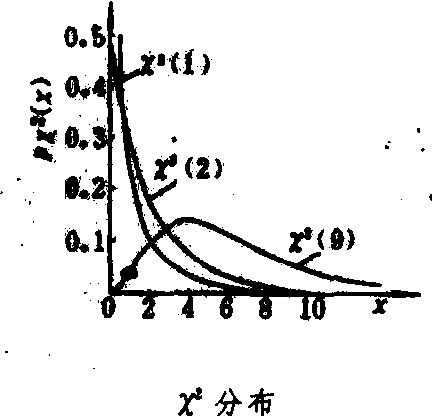
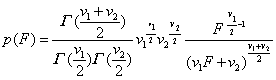
式中 v₁和v2分别为F的分子S²¹和分母S₂²的自由度，是p(F)的两个参数。F分布的定义域(0,∞),F分布曲线是随v₁和v₂不同而异的一组曲线，通常是偏斜的（见图）。

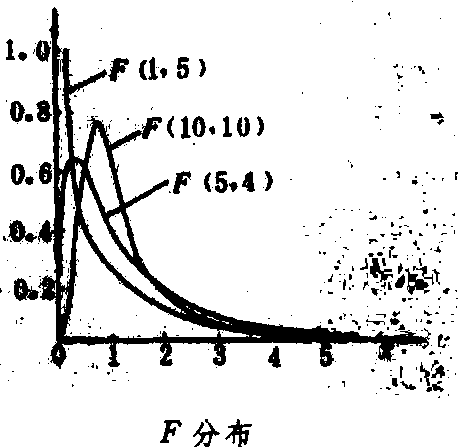
抽样分布

统计量的分布。常被应用于测验分数统计中。

抽样分布sampling distribution

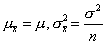又称样本分布。全称随机抽样分布(random sampling distribution)。从一个总体中，按一定的样本容量，随机地抽出全部所有可能的样本，由每个样本计算出的某一个统计数所组成的一种分布。例如在一个平均数为μ，方差为σ²的正态总体中抽祥，样本容量为n，则每个样本可以得到一个样本平均数_i。当抽出全部所有可能的样本后，则这些_i也可组成一个新的正态分布。 其参数。这里，μ和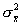分别为平均数抽样分布总体的平均数和方差。

抽样分布chouyang fenbu

指在众多的样本中某种统计量（如平均数或标准差）的分布。如在一个总体中抽取n=30的许多个样本，一个样本就有一个平均数，这许多样本的平均数的分布，就是一种抽样分布。
抽样分布有几个定理：若在总体中抽取容量为n的一切样本，则：
❶样本平均数的平均(μx)等于总体平均数，即：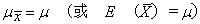

式中 ——样本平均数
μ——总体平均数
E——期望值（或所有统计量的平均值）

❷样本平均数的标准差(S)等于总体标准差除以n的方根，即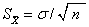

式中 σ——总体的标准差
n——样本容量
显然，亦有Sx2=δ2/n。

❸当n为大样本(如n≥30)时，样本平均数的分布近似于正态分布。
由定理
❸可知：当总体分布为正态时，样本平均数的分布也是正态的；当总体分布不是正态时，样本平均数的分布仍趋于正态，而且样本容量愈大，样本平均数的分布愈接近于正态。
上述定理在统计推断中有重要应用。

抽样分布Sampling Distribution

统计量的概率分布。一个统计量在统计分析中的优劣，主要根据其抽样分布来评定。最常用的有Χ²分布、t分布、F分布。

抽样分布

sample distribution

抽样分布sampling distribution

亦称“统计量分布”、“随机变量函数分布”。从某一总体中随机抽取的样本的统计量的分布。样本统计量有多种：如平均数X、标准差S、相关系数r、回归系数bxy、中数Md、众数Mo等。常见的抽样分布有二项分布、正态分布、t分布、X2分布及F分布等。上述各种统计量的分布是根据一定的数学理论推导而来，故又称理论抽样分布。另外还可根据观察或试验数据编制经验或试验的抽样分布。

抽样分布sampling distribution

样本统计量概率的理论分布。样本统计量主要有： 平均数、两个平均数之差、方差、标准差、相关系数、回归系数、百分比等。不同样本统计量具有不同的抽样分布，常用的有： 正态分布、t分布、F分布和χ²分布。统计量是基本随机变量的函数，故抽样分布亦称“随机变量函数的分布”。是统计推论的重要依据。

抽样分布

样本统计量的理论分布。常用的有正态分布、t分布、F分布和χ²分布。