投入产出法input-output methods

研究经济系统各部分投入与产出之间数量依存关系，特别是国民经济各部门在产品生产与消耗之间数量依存关系的一种经济数量分析方法。投入指进行某项经济活动的消耗，如生产活动中消耗一定数量的原材料、辅助材料、燃料、动力、设备等。产出指从事经济活动的结果，如生产活动中得到的产品等。20世纪30年代，列昂季耶夫(W.W.Leontief)在前人工作的基础上提出了投入产出法，并编制了美国经济1919年和1929年的投入产出表。第二次世界大战末期，这个方法受到美国政府重视。1949年，美国劳动部和空军合作，编制了美国经济1947年投入产出表。20世纪50年代以后，已有90多个国家先后编制了投入产出表。中国已编制1973年、1979年、1981年、1983年、1985年和1987年六个报告期国民经济投入产出表。
类别 按照分析时期的不同，可分为静态模型和动态模型。前者分析某一特定时期（通常是某一特定年份）的再生产过程。后者则分析若干时期的再生产过程及其相互联系。按照应用范围，可分为世界模型、多国模型、全国模型、地区间模型、地区模型、部门模型及企业模型。按计量单位不同，可分为价值型投入产出模型、实物型投入产出模型、劳动型投入产出模型和能量型投入产出模型。按照资料的性质和内容，投入产出表可分为报告期投入产出表与计划期投入产出表。前者是根据某一报告期实际数据编制的，后者则为计划数据。
静态投入产出模型 静态投入产出模型的基本结构如表1所示。表中假设国民经济分为农业、轻工业、重工业、建筑业、运输业、商业及服务业六大部门。从表的每行看，按照经济用途，总产品可分为中间产品和最终产品。前者指本时期内尚需在生产领域进一步加工的产品，如炼铁用的铁矿石、焦炭、电力、耐火材料等。由于从整个社会看，它们处于中间加工阶段，所以称为中间产品。后者指本时期内供居民个人消费、国家和集体消费、增加库存和储备、增加固定资产和净出口的产品。从表的每列看，各部门产品价值是由劳动对象的转移价值（中间投入）、固定资产折旧和新创造价值（最初投入）三部分组成的。
一般情况下，假设整个国民经济分为n个部门，则从每行看，有如下关系：

式中 X_i为第i部门产值；Y_i为第i部门最终产品价值；X_ij为第j部门生产过程中所消耗的第i部门产值。从每列看，有：

式中 D_j、V_j、M_j分别表示第j部门生产过程中发生的固定资产折旧额、劳动报酬和纯收入数额。
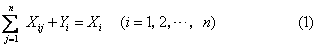
直接消耗系数 通常用a_ij表示，它反映在每单位第j部门产品生产过程中所消耗的第i部门产品数量，即：

直接消耗系数的大小取决于：❶该部门的技术水平和管理水平；
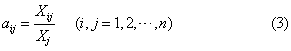
❷产品结构；
❸产品比价的变动。引入直接消耗系数后，(1)式可写为：

写成矩阵形式，AX+Y=X，式中A= {a_ij} n×n为直接消耗系数矩阵，X=(X₁,X₂，…，X_n)^T为总产出列向量；Y=(Y₁,Y₃，…，Y_n)^T为最终产品列向量。由此式可得出：

式中 I为单位矩阵。由于A具有以下两个性质：所有元素均为非负，即a_ij≥0;
❷每列之和小于1，即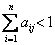，可以证明(I—A)为满秩矩阵，由此可得：

X=(I-A)^-1Y (6)

引入直接消耗系数后，(2)式可写为：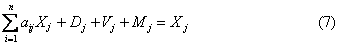

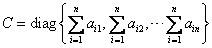改写成矩阵形式，CX+D+V+M=X 式中，为对角矩阵，D、V、M分别表示固定资产折旧额列向量、劳动报酬列向量、纯收入列向量。由此得出(I-C)X=D+V+M。可以证明I-C为满秩矩阵，得出：

X=(I-C)^-1(D+V+M) (8)

完全消耗系数 说明在单位最终产品生产过程中所直接和间接消耗的各部门产品的数量。以bij表示第j部门单位最终产品对第i部门产品的完全消耗系数，其计算公式为：

改写成矩阵形式，B=A+A²+A³+A⁴+…，式中，B={b_ij}n×n为完全消耗系数矩阵。可以证明，由于A具有上述两个性质，故有(I-A)^-1＝I+A+A²+A³+…，可得出B=(I-A)^-1-I。

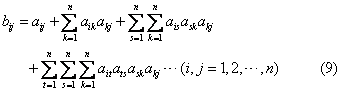
表1 简化的价值型投入产出表　单位：亿元

中 间 产 品

最 终 产 品

1 农业

2 轻工业

3 重工业

4 建筑业

5 运输业

6 商业及 服务业

小计

消费

投 资

增加储备

小计

总产品

生产性

非生产性

中 间 投 入

1. 农 业 2. 轻工业 3. 重工业 4. 建筑业 5. 运输业

X11 X21 X31 X41 X51

X12 X22 X32 X42 X52

X13 X23 X33 X43 X53

X14 X24 X34 X44 X54

X15 X25 X35 X45 X55

X16 X26 X36 X46 X56

Y11 Y21 Y31 Y41 Y51

Y12 Y22 Y32 Y42 Y52

Y13 Y23 Y33 Y43 Y53

Y14 Y24 Y34 Y44 Y54

Y1 Y2 Y3 Y4 Y5

X1 X2 X3 X4 X5

商业及 6.服务业 小 计

X61

X62

X63

X64

X65

X66

Y61

Y62

Y63

Y64

Y6

X6

最 初 投 入

固定资产折旧

D1

D2

D3

D4

D5

D6

新 创 造 价 值

劳 动 报酬

V1

V2

V3

V4

V5

V6

纯收入 小 计

M1

M2

M3

M4

M5

M6

合 计

总 投 入

X1

X2

X3

X4

X5

X6

完全需要系数 说明为得到某部门单位最终产品对各部门产品的完全需要量（包括直接需要量和间接需要量），其计算公式为：

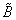式中 表示完全需要系数矩阵。
动态投入产出模型 主要有列昂季耶夫动态投入产出模型、大道模型和半动态投入产出模型等。列昂季耶夫动态投入产出模型为：

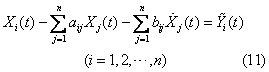
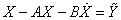式中 X_i(t)表示t时期第i部门产值；X_j(t)为X_j(t)对时间t的一阶导数；b_ij为资本系数，即第j部门为生产单位产品所占用的第i部门产品作为生产资本的数量，_i(t)为最终净产品数量，即扣除生产性投资以后的最终产品数量。模型中_i(t)为外在变量。上式可改写成矩阵形式，列昂季耶夫动态投入产出模型是一个线性一阶常微分方程组。其特征方程|I-A-λB|=0的n个根中可能出现复根，且必然成对出现。这时，模型的解中就可能包含余弦函数项。据此，资本主义国家部分经济学家曾用以解释资本主义社会生产不断发生周期性波动的原因。
上述动态模型可写为差分方程组形式：

其矩阵形式为X(t)-AX(t)-B〔X(t+1)-X(t)〕=(t)。该模型有两个重要假定：❶结构系数a_ij、b_ij在所讨论的时间区间范围内固定不变；
❷投资的提前期均为1年，即t+1年新增产量所需投资应在第t年投入。可用来研究动态逆矩阵以及资本形成过程中的时滞问题。
农业投入产出模型 农业是投入产出应用的重要领域。中国科学院系统科学研究所设计和编制了全国农业投入产出模型。该模型分为实物型、价值型、能量型三种。其基本结构如表2所示。农产品分为商品产品和非商品产品，国家要求按总产量和商品产量分别实现农产品供求平衡。据此，农业投入产出表每行应包括：❶农业中间产品，即农业生产过程中消耗的农产品；
❷农村自留，包括农民自给性消费及增加库存两部分；
❸非农业中间产品，如社会收购量中用于工业消耗的部分等；
❹商品产品中的最终产品部分，如用作城镇消费，返销农村，增加库存和国家储备、进口、出口等。该模型不仅包括投入部分，而且包括占用部分。前者有： ❶农业投入，即农业生产过程中消耗的农产品数量；
❷非农业投入，即农业生产中消耗的化肥、农药等非农业产品；
❸最初投入，包括固定资产折旧、劳动报酬、农业税、公积金、公益金、纯收益等。后者包括：❶占用土地数量；
❷占用固定资产数量；
❸占用流动资金数量；
❹占用劳动力数量。农业投入产出表可用于分析主要农产品成本和纯收益以及农业副产品的使用去向等问题。

表2 全国农业投入产出模型（简表）

			非商品部分		商品部分
			农业中间产品	农村自留	非农业中 间 产 品	最终产品	平衡差等	总产出
			1. 稻谷 … n.渔业	自给性消费 …	纺织工业 食品工业 …	城镇消费 销售农村 …
投 入 部 分	农 业 投 入	1.稻谷 ⋮ n.渔业
	非农 业投 入	1. 氮肥 ⋮
	最 初 投 入	固定资产折旧
		劳动报酬 ⋮
	总 投 入
占 用 部 分	播种面积
	固 定 资 产	1. 大中型 农用拖拉机 ⋮
	流动资金
	标准劳动日

投入产出模型研究的发展方向主要是：与运筹学中线性规划、非线性规划、动态规划、多目标规划等分支结合，编制最优化模型；研究理论上较完善而实际上又可行的动态投入产出模型：构造和估计最终产品和最初投入的经济计量方程组与投入产出模型形成有机联系；利用电子计算机自动编表等。

投入产出法input-output method

又称投入一产出分析。研究国民经济各部门(或地区、企业各部门)投入和产出之间数量依存关系的一种科学的定量分析方法。20世纪30年代由美国著名经济学家列昂节夫(W.Leontief)首先倡导应用。其要点为：根据统计资料，将国民经济各部门的投入来源和产出去向制成一种棋盘式的投入产出表，并把各部门之间产品量的依存关系用代数方程式表示出来，通过求解线性方程体系，可以推断某一部门产销情况的变化对其他部门的影响，计算出各部门应生产的产品数量。这种方法涉及的范围较广，变量甚多，且相互关系较为复杂，常需借助于电子计算机等工具求解。投入产出法常用于制订国民经济计划，进行中长期经济预测和经济分析。

投入产出法

见“国民经济管理”中的“投入产出分析”。

---

投入产出法

又称“部门联系平衡法”或“产业关联”。由美国经济学家瓦·列昂节夫(W.Leontief)20世纪30年代提出。研究国民经济各部门之间结构模型——投入产出模型。分为实物型和价值型。在经济发展比较稳定的情况下，可以进行定量预测，还可用于研究部门内部、地区之间、国家之间的经济联系。

投入产出法input-output method

是研究国民经济各部门（指产品部门）或地区、企业内部各部门各种产品生产与消耗之间数量相互依存关系的一种数学方法。此法可以用于经济预测、研究政策对经济发展的影响，为编制发展经济计划提供依据，以及研究人口、就业、环境污染、产品价格等社会、经济问题。

投入产出法

亦称“投入产出技术”、“部门联系平衡法”、“投入产出分析”或“产业关联法”。指利用一定的经济数学方法，借助电子计算机研究各种经济活动投入和产出之间的数量关系，并用来进行经济分析和经济预测的一种科学方法。投入是指在生产过程中输入的劳动对象、劳动资源和活劳动的数量，产出是指生产活动最终产出的成果，即产品的分配使用去向及其数量。进行投入产出分析，首先要把各生产部门的投入和产出及其相互关系，纵横交错地编制成投入产出表（可以价值和实物分别表示），然后，根据投入产出表的平衡关系，建立投入和产出的数学模型，最后，利用此类表和模型进行计划平衡、经济预测和经济分析。它既是一种进行部门（产品）间综合平衡的计划方法，又是一种预测未来的经济预测方法，还是一种对经济结构、经济效益、经济政策和商品价格等经济问题进行综合分析的经济分析法。
投入产出法是1936年由美籍俄侨列昂节夫(W.Leontief)首先提出的，随后，在美国、苏联、西欧、日本等国相继推广，现在全世界已有近百个国家编制了投入产出表。它不仅用于国家、地区、部门、城市和企业，而且，还可用于各大洲及整个世界。
在我国，推广它并不算迟，但真正应用它还是在1974～1976年间，编制了国家一级的投入产出表。现在，除了编制全国性的投入产出表外，山西、广东、黑龙江、河南、上海、北京、天津等省、市和冶金、化工、轻工、纺织、石油、煤炭等部门的一些企业，也在积极推广应用，并取得了可喜的成就。1983年6月在山西太原召开了全国投入产出法应用经验交流会。

投入产出法Input-output Method

参见“投入产出分析”。

投入产出法

作为一种分析工具与方法的投入产出表和相应的投入产出数学模型。参见“投入产出表”。

投入产出法

通过数量分析来表示和研究一个国家、一个地区、一个产业部门或一个基层企业的物质生产和消耗在各类经济体系中的相互依存关系的经济数学方法。投入，是指物质生产部门在产品生产过程中所消耗的原材料、燃料、动力、固定资产折旧和劳动力； 产出，是指生产出来的产品使用的方向和数量。
投入产出法的主要内容是根据投入产出原理来编制投入产出表(投入产出表的设计，是根据编表者需要研究和解决的主要问题，如核算价格、劳动消耗和经济效益等来确定的)。投入产出表编成以后，按照一定的计算公式，对表内所列数据进行计算，即可揭示经济体系中各部分之间错综复杂的技术经济联系以及国民经济的各项重要比例关系，为加强综合平衡和改善经济结构提供重要的数量依据。
国民经济是个有机整体，它的主体是由各个物质生产部门及其归属下的若干产业部门构成的。这些部门之间存在着十分复杂的相互依存的数量关系。这样复杂的数量关系，用一般的统计方法或计算手段是不容易解决的。投入产出法是解决这一问题的有力工具。通过编制和应用投入产出表，可以比较准确地计算出国民经济各个部门之间的技术经济联系，用数量反映出它们之间的依存关系，为编制国民经济计划提供可靠的依据。
投入产出法的应用范围很广，它可应用于研究企业管理、价格形成、劳动消耗、经济效益等许多方面。

投入产出法

亦称“部门联系平衡法” ，是从经济体系的整体出发，分析各部门(或地区、单位)间生产与消费的数量依存关系的方法。投入产出法的主要内容包括投入产出表和相应的数学模型（或称线性方程体系）。投入产出法是把国民经济各部门在一定时期的投入来源和产出去向排列成纵横交错的棋盘式表格式。投入产出法概括了整个国民经济的经济联系，它不但反映了社会产品的实物形成过程，而且反映了社会产品的价值形成过程。编表后，可以利用数学方法和电子计算机计算出直接消耗和完全消耗系数以了解各产品生产与消耗之间的直接技术经济联系和所有的间接联系。

投入产出法

通过平衡方程，借用数学模型分析初始投入、中间投入、总投入和中间产品、最终产品、总产出之间的关系。模型核心是Leontief逆矩阵，它反映了其中各个流量的来源和去向。自20世纪30年代，W ·Leontief首次提出投入产出表，投入产出分析法( IOA,Input Output Analysis) 已经发展成当代经济学理论与实践的一个重要的分析工具。早期的投入产出分析从可持续发展的观点来看，存在着两方面的缺陷： 同国民经济核算体系中其他核算理论方法一样，现有投入产出核算及其基本核算表式设计均是建立在纯经济系统分析基础之上，对与经济活动有密切相关的 （自然） 资源、环境系统并未加以考虑，其投入产出仅考虑了经济活动纯经济性一面，而没有计入由于经济活动所造成的资源、环境损耗以及由此而引发的资源、环境保护活动等经济活动社会性的一面； 作为流量核算方法，投入产出核算及基本核算表式设计均局限于纯流量核算分析的范围，而对与流量密切相关的存量及其与流量之间相互关系核算问题并未涉及。
由于经济外部性的存在，现实中经济活动同自然资源、环境之间存在着相互影响。其中相互作用的负反馈机制主要是任何一项经济活动的成本代价，不仅包括对各种生产要素的消耗，而且也应包括由于其外部不经济而对自然所造成的代价。投入产出分析的应用领域正在逐步扩展，与资源、环境相关的投入产出分析法正在逐步受到重视。由于投入产出分析法对构成整个经济结构的个体之间相互关系的关注，使得它成为工业生态学一个重要的分析方法，应用到对各种不同尺度、不同拓扑结构的工业经济系统的分析中，它的对象从货币流扩展到物质流、能量流，其中应用较为广泛的就是实物型投入产出表。实物型投入产出表方法描述自然资源进入经济系统、被加工为产品、作为商品被使用以及最终以废弃物的形式回到环境的整个过程。实物型投入产出表的基本用途是平衡、校核、推估数据以及作其他模型 （或分析） 的基础。实物型投入产出表法也可用于物资流分析，不仅揭示经济活动中的直接和间接物质投入，也可揭示生产、消费过程中的非直接负荷。实物型投入产出表需要大量的数据，编制起来耗时费力、成本高，每隔若干年能做一次就不错。实物型投入产出表方法在德国和丹麦得到了广泛应用，这两个国家都完成了1990年的实物投入产出表的编制。另外，荷兰编制了1990年水泥、造纸、钢材等项物资的实物投入产出表，芬兰于1995年、日本于1990年也完成了部分物资的实物投入产出表的编制。国内还没有编制出实物投入产出表。

投入产出法

亦称“投入产出分析”。将经济理论、数学和统计学结合在一起，通过编制投入产出表，建立相应的经济数学模型，对经济系统各个部分(作为生产单位或消费单位的产业部门、行业和产品等) 间表现为投入与产出的相互依存关系进行经济数量分析的方法。在商品经济条件下，经济系统各个部分间投入和产出的相互依存关系表现为商品交换关系，即作为商品的相互购买者，作为资源的占用或使用者，作为销售者售给最终消费者等的相互关系。这种数量分析方法，最初是由研究一国的国民经济各个产业部门间的联系发展起来的，因而也被人们称为“部门联系平衡法”、“产业关联法”等。但实际上它的应用范围十分广泛，大至国际经济关系，小到一个企业的生产经营活动，甚至在经济领域之外，只要某种事物在最广泛的意义上有投入和产出，原则上都可应用投入产出分析。无论应用在哪里，各种形式的投入产出模型的共同特点是通过一个确定的线性方程组，以系统的各个部分间客观存在的工艺技术联系为基础来描述它们之间的数量依存关系。除了数学模型，投入产出表也是它的基本形式。表的内容反映着系统各部分运动的来龙去脉，具有较强的解释和分析功能。投入产出法产生于20世纪30年代，美国经济学家瓦西里·列昂惕夫于1936年发表了投入产出法的第一篇论文。半个世纪的发展，其成就表现为： (1)基本原理方面，外生变量内生化，静态模型向动态模型发展。在静态模型建立的最终产品和总产品联系的基础上，动态模型进一步建立了上期投资和下期产出变化的联系，使投资需求由静态的外生而变为动态的内生。系数的修订和预测方法得到发展。投入产出法和优化方法结合，建立投入产出的优化模型。(2)应用的广度方面，投入产出法很早就已经作为地区分析的方法加以应用，它还用于核算劳动、固定资产和投资以及核算环境污染等。目前，各国仍在作出各种努力扩大投入产出法的应用范围。随着投入产出法的产生和发展，它在国民经济计划和管理中起着日益重要的作用，改进并健全了国民经济核算体系，广泛和深入地用于分析和论证各项经济政策及其影响，进行一致性预测和国民经济计划的综合平衡。投入产出法有两个基本假定，即同质性假定和比例性假定。前者是假定每个部门只生产一种产品，并只用一种工艺技术方式生产，而且不同部门产品之间不存在相互替代的现象。后者是假定每个部门的投入是该部门产出的线性函数。这两个假定适应建立投入产出数学模型的要求，但同实际情况有较大的差距。在作长期预测或在经济转折时期，在技术进步和经济结构变动较剧烈的条件下，投入产出法在反映国民经济的运转时所产生的误差尤为明显。(参见“投入产出表”、“经济数学模型”)

投入产出法

input-output method