异面直线距离的一种计算公式
异面直线距离的一种计算公式yimian zhixian juli deyizhong jisuan gongshi
如图1,设l,m为两条异面直线.过m作两个平面α,β分别交l于A,B.点A到m的距离AC=a,点B到m的距离BD=b.二面角α-m-β为θ.则异面直线l,m的距离为
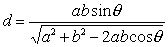
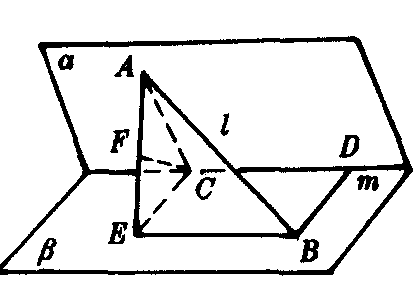
图1
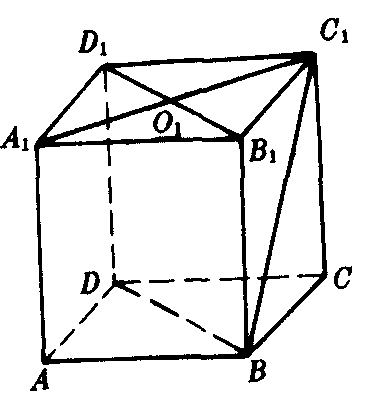
图2
证 在平面β内过C作CE⊥CD,过B作CD的平行线与CE交于E,则∠ACE=θ,CE=b,连结AE.容易证明平面ACE⊥平面AEB.在平面ACE中,作CF⊥AE于F,则CF⊥平面AEB,即CF是C点到平面AEB的距离.因为CD∥平面AEB,所以CF是CD到平面AEB的距离,也就是l到m的距离.
在△ACE中,因为
AC·CE·sinθ = CF·AE
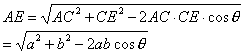
| 所以 |
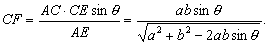
例 如图2,正方体ABCD-A1B1C1D1的棱长为a.求B1D1与BC1间的距离.
解 作对角面BD1,则B1D1是平面BD1与平面B1C1D1的交线,连结A1C1.设A1C1∩B1D1=O1,则C1O1
| ⊥B1D1 |
| 即C1到B1D1的距离为 |
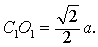
| 而B到 |
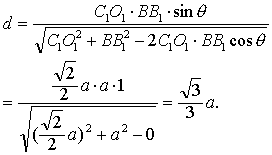
☚ 两条异面直线的距离 异面直线上两点间的距离公式 ☛
- 三絶是什么意思
- 三綽是什么意思
- [三]繁体字简化的方式是什么意思
- 三红是什么意思
- 三红吟馆是什么意思
- 三红子是什么意思
- 三红汤是什么意思
- 三红药油丸是什么意思
- 三级是什么意思
- 三级五方联审的政审方法是什么意思
- 三级价格歧视是什么意思
- 三级会议是什么意思
- 三级保养是什么意思
- 三级保养制是什么意思
- 三级偏旁是什么意思
- 三级八一勋章是什么意思
- 三级公路是什么意思
- 三级军士长是什么意思
- 三级农机修造网是什么意思
- 三级制是什么意思
- 三级制两股绳是什么意思
- 三级制和两股绳院校训练体制是什么意思
- 三级医疗预防网是什么意思
- 三级协同是什么意思
- 三级命题制是什么意思
- 三级培训体制是什么意思
- 三级复句类是什么意思
- 三级复核制度是什么意思
- 三级妇幼保健网是什么意思
- 三级安全教育是什么意思
- 三级审稿制是什么意思
- 三级审稿制度是什么意思
- 三级审签制度是什么意思
- 三级小说是什么意思
- 三级市场是什么意思
- 三级干部会议是什么意思
- 三级循环反应阶段是什么意思
- 三级战备是什么意思
- 三级所有、队为基础是什么意思
- 三级所有制是什么意思
- 三级所有队为基础是什么意思
- 三级所有,队为基础是什么意思
- 三级批发商店是什么意思
- 三级护理是什么意思
- 三级护理制是什么意思
- 三级教练员是什么意思
- 三级教育是什么意思
- 三级机场是什么意思
- 三级板是什么意思
- 三级核算是什么意思
- 三级武士是什么意思
- 三级浪高鱼已化,九霄路远鹏方息。是什么意思
- 三级渠道是什么意思
- 三级火箭是什么意思
- 三级片是什么意思
- 三级独立自由勋章是什么意思
- 三级环流是什么意思
- 三级科技咨询体系是什么意思
- 三级税是什么意思
- 三级结构是什么意思