带余式除法定理
带余式除法定理daiyushi chufadingli
对于数域F上任何两个多项式bm≠0其中(x)≢0，存在F上唯一的一对多项式q(x)及r(x)，满足下列条件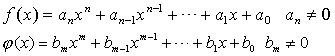
❶r(x)的次数小于m，或者r(x)≡0;
❷恒等式f(x)≡q(x)(x)+r(x)成立.
多项式q(x)和r(x)各叫做不完全商及余式.这个定理是一元多项式分解理论的基础.
q(x)及r(x)的求法叫做多项式f(x)被(x)除的带余式除法.
显然，要使多项式f(x)能被(x)整除，其充分必要条件是f(x)除以(x)时所得的余式恒等于零.
☚ 非当然因式 不完全商 ☛
- 女劳疸是什么意思
- 女劳黄疸方是什么意思
- 女劳黑疸方是什么意思
- 女包是什么意思
- 女化蚕是什么意思
- 女匠是什么意思
- 女匪是什么意思
- 女医是什么意思
- 女医生是什么意思
- 女十五岁是什么意思
- 女十忙是什么意思
- 女十忙图是什么意思
- 女十忙圖是什么意思
- 女华是什么意思
- 女单是什么意思
- 女博士是什么意思
- 女博士索菲·柯瓦列夫斯卡娅的遗恨是什么意思
- 女厕所是什么意思
- 女厝是什么意思
- 女又十一撇儿是什么意思
- 女又十撇是什么意思
- 女又十撇儿是什么意思
- 女友是什么意思
- 女友门是什么意思
- 女双是什么意思
- 女反派角色是什么意思
- 女叔是什么意思
- 女受施者是什么意思
- 女叙是什么意思
- 女口是什么意思
- 女口不役之制是什么意思
- 女古是什么意思
- 女古斡鲁朵是什么意思
- 女古没里是什么意思
- 女古滂是什么意思
- 女古烈详稳司是什么意思
- 女史是什么意思
- 女史吟是什么意思
- 女史彤管是什么意思
- 女史箴是什么意思
- 女史箴图是什么意思
- 女史箴圖是什么意思
- 女史篇是什么意思
- 女史花是什么意思
- 女司售人员的劳动卫生是什么意思
- 女合是什么意思
- 女合承分案是什么意思
- 女吊是什么意思
- 女同事是什么意思
- 女同学会是什么意思
- 女同性恋者的女权运动是什么意思
- 女同桌只留给了我一颗痣是什么意思
- 女后是什么意思
- 女吏是什么意思
- 女君是什么意思
- 女君王 (女皇帝)是什么意思
- 女呃是什么意思
- 女和尚是什么意思
- 女咯是什么意思
- 女哩是什么意思