对策论

又称“博弈论”，数学的一个分支。它分析在竞争的环境下，其结果不仅依赖于一个人自己的决择及机会，而且依赖于其他参与者的决择。这样，竞争的结果依赖于所有参与人的行为，每个参与人都期望预测其他参与人的可能的决择，以确定自己的最佳对策。如何合理地进行这些相互依赖的战略策划就是对策论的主题。该理论产生于40年代，现已应用于经济、政治、军事、运筹学、商业、法律、体育、生物等领域。在对策论中有一个著名的犯人的二难推理：假设两个商业合伙人因逃税而被捕，检察官将他们隔离审问，并允诺若两人都承认可减刑但不能得到报酬；若一人承认另一人不承认，承认者得到报酬并获得自由，不承认者被监禁；若两人都不承认，都可获释。这时合伙人应采取何种对策？从双方来讲，最好的结果是都不承认而获得自由；但是谁都不能肯定另一方不承认，因为他们都知道另一方如果承认而自己不承认时方可得到报酬并威胁到自己的自由；采取承认的策略，又考虑到若双方都不承认，可使双方都获释。而事先双方无时间协调对策。这样双方就处于一种非确定性的对策选择。对策论可分为：(1)2人对策与几人对策；2人对策研究2人参与者的最优策略决择；n人对策(n>2)主要讨论何种结盟将会形成并成为稳定的；(2)零和对策与非零和对策：前者每次结局时给参与者支付总和是零（或某个常数），而后者支付总和是可变的；(3)合作对策与非合作对策：前者的参与人可以达成具有约束性和强制性的协定，而后者可以允许也可以不允许参与人之间的协商。对策论的所有领域都假设参与人是理智的，即他们都希望在竞争中获胜，他们都具有各自的目标，能分辨不同竞争结果的优劣。

对策论game theory

研究对策现象的数学理论和方法，也称博奕论。对策是决策者在竞争状态下进行的决策，是参加竞争的各方为了自己获胜而采取的对付对方的策略。1944年冯·诺伊曼(J.vonNeumann)和摩根斯特恩(O.Morgenstern)合著的《对策论与经济行为》对对策论进行了系统的研究。开始应用到经济方面，并逐步扩展到军事、政治学、心理学等领域。
任何一个对策活动都包括三个基本要素： 局中人、策略和得失函数。参与竞争活动的各方称为局中人。局中人可以是个人或组织。策略指局中人据以选择其行动方案的规则，全部策略称为策略集。假定局中人都是明智的，并且都知道对方的策略集。如策略个数有限，为有限对策，否则为无限对策。得失函数是用数量表示的对策结局。从每个局中人的策略集中各取一个策略组成的一个策略组，称为局势。对策分为静态对策和动态对策。静态对策可按局中人的数量、有无结盟、策略数是否有限以及得失之和是否为零来分类。动态对策有多阶段对策、微分对策等。
二人有限零和对策 设局中人为甲、乙双方，分别有m和n个策略，在任一局势中全体局中人的得失相加总是等于零。其得失可用赢得矩阵表示(表1)。

表1 对策赢得矩阵

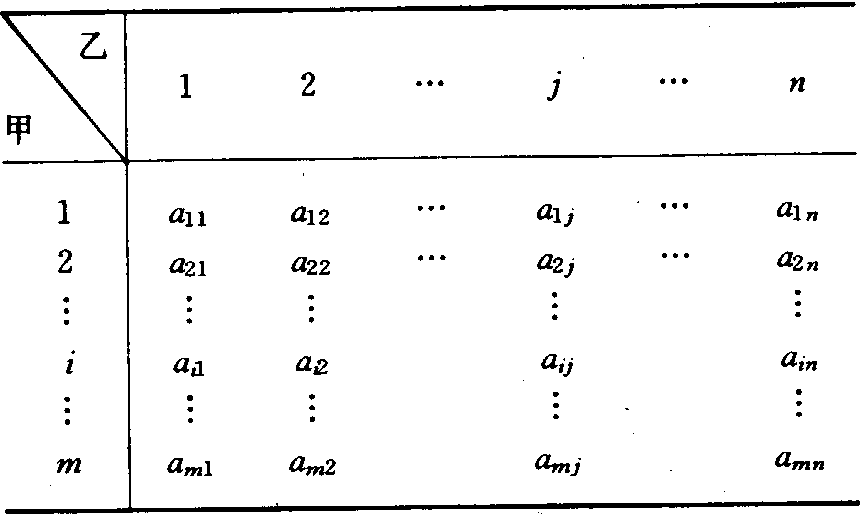
矩阵中a_ij为一方的（例如甲）赢得值。当甲取策略i，乙取策略j时，甲之得为a_ij，而乙之得为-a_ij，故a_ij+(-a_ij) =0，称为二人零和对策。
二人零和对策还可分为纯策略解与混合策略解。❶纯策略解。双方规定不管对方采取什么方案，各方总是采用一种方案。例如，假定局中人甲有两个行动方案a₁和a₂，局中人乙也有两个行动方案b₁和b₂可供选择。二人对局构成一个赢得矩阵。矩阵中的赢得值表示甲赢得乙的钱数。这类问题可以根据最大最小理论用悲观准则求解。如表2所示。

表2 纯策略求解过程 (单位：元)

甲 乙	b1	b2	行最小值
a1 a2 列最大值	200* 100 200*	250 300 300	200* 100

注：*表示甲、乙双方对策方案。

在本例中甲如果选a₁，最少能赢得200元，如选a₂，最少能赢得100元。按小、中取大准则选a₁，至少赢得200元。对于乙方，他希望损失最小，因此乙如选b₁最多付出200元，如选b₂，最多付出300元。按大中取小准则选方案b₁，至多付出200元。最终结果是甲选a₁，乙选b₁，对策解为200元。此值恰等于行最小值中的最大值和列最大值中的最小值，称为鞍点。这种对应于鞍点的策略，称为最优纯策略。
❷混合策略解。如果在二人零和对策中找不到一个双方都满意的可重复采用的策略，就成为无鞍点的二人零和对策，此时必须采用混合策略求解，即在重复对策时各方必须交替采用不同方案。例如，甲、乙两公司在推销产品的活动中，甲公司采取a₁和a₂两种方案，乙公司采取b₁和b₂两种方案，构成赢得矩阵。矩阵中的赢得值表示市场占有率(%)。正值表示甲赢得而乙失去的值，负值表示甲失去而乙赢得的值。假定用悲观准则求解，如表3，结果是甲选a₁，乙选b₂。没有鞍点。这种情况下双方不能重复采用一种方案，而必须采取混合策略。例如，甲先选a₁，乙将选b₂。当甲发现乙选b₂时，甲将转向a₂，这样甲将获得比a₁大的赢得值。当乙发现甲转向a₂，必然转而选b₁，于是甲又将转向a₁，等等，双方将会发现，改变方案比总是采用一种方案要好。平均赢得值由双方采用各方案的次数比例决定，而且在某一比例时对各方都是最好的。本例的最终结果：甲公司选a₁、a₂的次数比为3:5；乙公司选b₁、b₂的次数比为1:3，甲的期望赢得值为1/4，乙的期望失去值也为1/4。局中人数m=2和方案数n=2的混合策略对策问题可用解析法或图解法求解，m≥2, n≥2的有限对策问题，可用线性规划法求解。

表3 混合策略对策问题

甲 乙	b1	b2	行最小值
a1 a2 列最大值	4 -2 4	-1* 1* 1*	-1* -2

非零和对策 在非零和对策中，局中人一方赢得的值不等于另一方失去的值。这意味着在环境中，某些参与者可能分担得失。所以非零和对策不是严格的竞争，因而具有合作的可能性，这样就使对策问题的求解过程变得更复杂，更不确定。因为在非零和对策中出现了心理状态、信息交流、讨价还价等行为因素，可能妨碍用数学方法来获得一个简单合理的解。所以非零和对策只能根据具体参加者的个人情况和需求来求解。
N人对策 N>2时对策的主要特点之一是联盟。局中人之间的关系逐渐稳定，成为两个对抗集团。这种情况下可以按二人对策问题求解。
微分对策 是连续时间的多阶段对策。状态转移可用微分方程描述。

对策论

亦称“博弈论”。研究对策现象的数学理论与方法。是运筹学的一个分支。中国古代对于对策现象早有研究，脍炙人口的“齐王赛马”就是一例。战国时期，齐国的田忌以下马对齐王的上马，然后以上马对齐王的中马，以中马对齐王的下马，结果一负两胜，赢得千金。军事上，作战的双方进行着你死我活的斗争，战争的胜负，既是双方战斗实力的较量结果，也是双方斗争策略较量的结果。高明的斗争策略可以弥补战斗实力的不足。对策论可以帮助我们同敌斗智，从数量上分析各种可能结果，做到胸中有数，力避最坏结局，夺取最大战果。

对策论

由于经济与军事的需要而形成的对策论属于应用数学的范畴。它是关于斗争的数学，主要是用数学方法研究斗争(包括战争、竞技、比赛，也包括人与自然的斗争)中是否存在制胜对方的最优策略以及如何寻找这些策略等问题。对策论的始祖可以追溯到中国战国时代的孙膑，但真正形成一门独立的科学，应以1944年冯·诺伊曼包括战争、竞技、比赛，也包括人与自然的斗争中是否存在制胜对方的最优策略以及如何寻找这些策略等问题。对策论的始祖可以追溯到中国战国时代的孙膑，但真正形成一门独立的科学，应以1944年冯·诺伊曼(Neuman,JohnVon)、摩根斯坦(Morgenstern,Oskar)合著的《博奕论与经济行为》(Theory of games and Economic Behav-ior)的尊基性工作为标志。目前，对策论已深入到经济、文化、教育等许多领域，如在工厂的管理、市场行为约束、球队比赛中都有应用。

对策论Game Theory

亦称博弈论。即用于分析竞争形势和竞争后果的一种数学理论。1944年美籍匈牙利数学家冯·诺伊曼和美籍奥地利经济学家O.莫根施特恩所著《对策论和经济行为》的发表，标志着现代对策论的诞生。自此之后，世界已有大量论著，论述和讨论其在经济、政治、军事、商业、法律、体育、生物以及其他领域的运用。学者们普遍认为，这一理论的提出，是人类智慧的巨大成就，它对于扩展和精炼战略思想起有重要的作用。这一理论把参加竞争的每一方(包括个人、公司、国家、集团等)，称为一个局中人。认为竞争的结果不仅取决于某个局中人的抉择，而且取决于其他局中人的行为，依赖所有局中人的行为。因此，每个局中人都企图预测其他局中人可能做出的抉择，以确定自己的最佳对策选择。如何进行这种相互依存的战略对策策划，正是对策论的主题。对策论最核心的内容包括：(1)2人对策与n人对策(n大于2)。2人对策研究在两个局中人竞争中如何做出最优战略抉择；n人对策主要研究在所有局中人中如何进行结盟，如何合理分配支付，如何在预测他人的抉择中做出自己最优的抉择。(2)零和对策与非零和对策。前者研究如何使竞争的结局能达到局中人的支付总和为零（或某个常数），即一个局中人所得，恰是另一个局中人所失，这是一种完全对抗性的对策；后者主要研究如何使竞争结局能达到局中人支付的总和是可变的，即使局中人能同时有所得或有所失。(3)合作对策与非合作对策。前者主要研究如何使局中人达成具有约束性和强制性的协定；后者主要研究可以允许或可以不允许局中人之间的协商；但总是假定任何达成的协定都处于平衡状态，即一个局中人在其他局中人不破坏协定的情况下，独自破坏协定是不理智的，因为这样做就会引起连锁反映，并使他的情况恶化。对策还有如下三种不同的表述方式或类型：(1)展开型（对策树）。指出局中人可以做出抉择的序列，而支付定于每个抉择序列的结尾；(2)常规或策略型。指出局中人能够采取的策略或依据其他局中人的抉择而确定的全部计划，对于各局中人所采取的策略的所有不同组合，以及同一个矩阵给出这些组合情况下各人所得的支付；(3)特征函数。指出所有可能的结盟对其他成员的价值。对策论的所有领域的一个共同假设是：局中所有的人都是理智的。即他们都希望在竞争中获胜，并且各有各自的目标，以及能够分辨竞争结果的优劣。然而，由于抉择的相互依存的关系，一个局中人不可能有直截了当的最佳选择。仅有的例外是退化的一人对策，有时称之为“与自然抗衡的对策”，这也是对策论的课题。

对策论

见“博弈论”。

对策论

利害冲突或利益冲突的双方在对抗性或竞争性的活动中，用数学方法研究是否存在自己战胜对方的最优策略，以及如何找出这些策略的一种理论，故亦称博弈论、竞赛理论或对局理论。最初对策论的研究集中于桥牌、棋艺等方面，1921年，法国人包瑞尔首先开始进行对策论研究。1928年美国数学家冯·诺意曼提出“最大最小原则”，为对策论的研究奠定了理论基础。目前，在军事、经济、心理等领域广泛应用，使对策论从对只有两方参加的竞争活动的研究发展到对多方参加的竞争活动的研究，这就包括主体行为的一方与诸方的错综复杂的对策研究，如完全对立、部分同盟部分对立、多方同盟与一方对立、同盟内部的合作与对立等等。活动要通过多次参加决策才可能有某种结局，而每次的决策研究都有可能出现新的变数，这又增加决策的难度。数学家根据支付函数形式分为离散和连续对策；根据支付情况分为零和对策和非零和对策；研究追赶现象的微分对策等。在分析对策现象时可以用支付矩阵（标准型）或对策树（展开型）等方法。

对策论Game Theory

也称为博弈论，是“研究决策主体的行为发生直接相互作用时候的决策及其这种决策的均衡问题的，也就是说，当一个主体，好比说一个人或一个企业的选择受到其他人、其他企业选择的影响，而且反过来影响到其他人、其他企业选择时的决策问题和均衡问题” (张维迎，1996,P.3～4)。如果一个对策中存在着具有完全约束力的协议 (Binding Agreement)，并且这种协议是可强制执行的，则该对策就是合作的(Harsanyi,J.,1966); 如果不存在这种协议，对策中的每一个参与人 (Player) 都从个人理性出发极大化其个人效用函数或极小化其支付函数，则该对策是非合作的 (non-cooperative)。如果一个对策中的每个参与人必须同时选择自己的行动，或在行动之前不能确知其他参与人采取了什么具体行动，则该对策是静态的 (Static); 如果一个对策中参与人能够了解先行者采取的行动，则该对策是动态的，动态博弈又包括具有或不具有完全信息的重复对策、随机对策、生存或毁灭对策、递归对策以及参与人变动对策等 (Luce,R.,1957)。如果一个对策中所有参与人的类型特征、战略空间以及支付函数均为常识，即每个参与人都知道它，参与人知道其他参与人知道它，则该对策是完全信息的 (Lewis,D.,1969); 如果参与人之间的信息是不对称的，即至少有一个参与人的信息不是常识，则该对策是不完全信息的。
对策论的起源以冯·诺依曼 (Neumann,V,1944) 出版 《对策论与经济行为》 为代表。除了对零和博弈 (Zero-sum Games) 和多人合作博弈进行了讨论以外，诺依曼对对策论的重大贡献在于三个方面： (1) 确定了对策论在经济学中的研究方法，即从个人效用函数及其约束条件出发，讨论个人通过何种战略达成效用极大化以及对策的最终均衡结果，这使得经济学逐渐放弃了一些缺乏微观基础的假定并越来越将其基础建立在对策论之上； (2)提出了最大最小定理，即在二人零和博弈中，每个参与人将极大化其效用函数而极小化其支付函数，因此如果参与人具有有限多个纯战略(Pure Strategy)，则该对策的均衡战略是确定的； (3)提出了等价性原理，即在“博弈参与人数变得真正很大时，某种希望将会出现，每个特定的参与者的影响变得可以忽略不计……因此，市场价格的建立是在市场上运转的基本力量自然地产生的，几乎不管我们假定这些力量是怎样运转的。” (但是和诺依曼共同提出等价性原理的莫根斯坦 (Morgenstern) 却认为由于参与人趋向于合作，因此完全竞争市场并不具有现实意义)。
早期对策论研究的重点在于零和博弈和合作博弈。在零和博弈中，除了已提到的最大最小定理外，泽梅罗定理 (Zermelo Doctrine) 称每一个完全信息的二人零和博弈其均衡结果是严格确定的，但是泽梅罗并没有指出参与人如何构建立正确战略。这两个定理在数学上具有严谨结构，但它们在解决理性决策问题上并无太理想的实际作用 (Colman,A.,1982)。在合作博弈中，诺依曼定义了即使在非合作博弈中也十分重要的预期效用和稳定集的概念，前者指当参与人采取混合战略时 (Mixed Strategy)，其效用成为预期效用； 后者是指博弈的可能均衡中，应排除劣战略 (Dominated Strategy)和在扰动下导致均衡变动的战略，这对后来纳什均衡 (Nash Equilibrium) 和颤抖手均衡 (Trembling Hand Equilibrium) 概念的出现有一定影响。诺依曼还考虑了可转移效用 (Transferable Utilities) 博弈中的均衡战略问题，所谓可转移效用博弈是指如果某联盟(Coalition)成功，则联盟中的参与人可以以任何方式进行总效用的分配，但这种分配受在联盟外的参与人行为的影响。例如三个参与人以多数票方式分配一个单位的总效用，可能均衡有 (1/2,1/2,0)、(1/2,0,1/2) 和 (0,1/2,1/2)，但这并不意味着结成联盟的两个人将第三个参与人排斥在分配之外，这是因为任何两个人都可能取得联盟的成功。从个体理性看，一个参与人加入联盟的可能性为2/3，在联盟中的预期分配效用是1/2，结果该博弈的最终结果是参与人在竞争压力下平均分配(1/3,1/3,1/3); 此后比莱拉 (Billera,L.,1970) 讨论了非转移效用理论的均衡问题，他研究的算法可以寻找出市场均衡状态的核心（即所有非劣战略的集合） 和一般映射的不动点，它常常被用于求解多个参与人的博弈中参与人权重 (也称沙普利值，Shapley,I.,1964) 与竞争均衡之间的关系。后来关于合作博弈的研究逐渐以非合作博弈方法建立合作博弈的一般理论以及投票机制的应用研究为主。
在50年代以后，非合作博弈的理论开始成熟并成为对策论的主流研究方向。纳什(Nash,J.,1950) 定义了在完全信息下静态博弈的均衡，如果参与人的战略组合满足这样的特征： 给定其他参与人所选择的战略维持不变的前提下，任何一个参与人都不能通过仅仅变动自己的战略而获得比原先更大的效用。纳什均衡似乎是一种僵局，任何参与人都宁愿维持而不是单独变动该状态。纳什同时还指出，在一个有限参与人和行动的博弈中，至少存在一个纳什均衡。德布鲁 (Debreu,G.,1952)和奥曼 (Aumann,R.,1987) 随后进一步讨论了完全信息静态博弈中的纳什均衡存在性和相关均衡等问题。稍后塔克发现了囚徒困境(Prisoner’s Dilemma) 揭示出个人理性和集体理性的冲突。库恩 (Kuhn,H.,1953) 为了证明在完全信息动态博弈中至少存在一个纯战略纳什均衡，提出了子博弈 (Subgame) 的概念，如果在任何时刻所有参与人都知道在此前发生的一切 （即参与人具有完美记忆），那么此后所发生的一切就可称为原博弈的一个子博弈，这和群论中原群和子群的概念极为类似；塞尔腾 (Selten,R.,1975) 扩展了库恩的结果，提出一个均衡 （可以是混合战略均衡）。如果既是原博弈的纳什均衡又在每一个子博弈上给出纳什均衡，则该均衡构成子博弈精炼纳什均衡 (Subgame Perfect Nash Equilibrium)。而无名氏定理 (Nash Folk Theorem) 则讨论了无限次重复博弈的纳什均衡问题，指出如果参与人具有足够的耐心（即时间贴现因子足够大），那么任何满足个人理性的可行支付集均可通过特定的子博弈均衡得到。直到哈萨尼(Harsanyi,J.,1967～1968) 提出哈萨尼转换(Harsanyi Transformation) 以后，非合作不完全信息博弈的研究才有了突破。转换思路是引入博弈虚拟参与人“自然” (Nature)，在博弈中自然首先行动并决定参与人的特征； 参与人不能确定除自己以外的其他参与人的类型，但是了解其他参与人的可能类型的概率分布函数，并将其当作博弈参与人共同知道的知识(Common Knowledge)，这样不完全信息就转变成完全但不完美信息，求解不完全信息静态博弈的均衡问题基本解决了； 如果参与人能够根据观察到其他参与人的行动来修正自己的后验观点和应采取的后续战略，则静态博弈中子博弈精炼纳什均衡就扩展为动态博弈的精炼贝叶斯均衡(Prefect Bayesian Equlibrium)，这种均衡在每一个后续博弈中均成立，并且均衡本身就是参与人利用贝叶斯法则不断修正自己的后验概率和战略的结果。塞尔腾(Selten,R.,1975) 则引入了颤抖手均衡 (Trembling-hand Equlibrium) 的概念，指出在一个均衡必须具有抗扰动性和自适应性，即参与人应该允许其他参与人犯错但是这种无意的错误不会导致均衡的破坏。哈萨尼和塞尔腾还合作对不完全信息博弈中的均衡及双人叫价模型进行了总结 (Harsanyi & Selten,1987)。目前博弈论几乎重塑了经济学的微观基础并导致了经济学研究方法的深刻变革，此外它在社会学、心理学、生物学及现代军事理论中亦有重要地位。

对策论game theory

数学中分析竞争行为的一个分支，参加竞争的每一方(个人、公司、国家、集团等)称为一个局中人。对策竞争的结果不仅取决于某个局中人的抉择，而且依赖于其他局中人的行为。因此，每个局中人都企图预测其他局中人的可能的选择，以确定自己的最优对策。如何在这种高度不确定性的相互制约关系中进行合理的战略策划，就是对策论的主题。
现代对策论的奠基性著作是美籍匈牙利数学家冯·诺依曼(J.Von Neumann)和美籍奥地利经济学家摩根斯特恩(O.Morgenstern)1944年发表的《对策论与经济行为》。对策一般依描述形式分为三种基本类型：展开型，策略型，合作型；依对策各方总得失之和是否为零（常数）分为零（常）和对策与非零（常）和对策；依是否允许局中人之间达成约束性协定分为合作对策和非合作对策；依局中人数目分为二人对策和n人对策。二人零和（常和）对策的理论已臻完善。对一般的n人对策提出过多种求解途径，但尚未确立统一的理论。n人对策的重要问题是研究在对策中将会形成何种稳定的结盟，以及在结盟成员中如何合理分配结盟所得。所以，n人合作对策吸引了许多学者的研究。

对策论

亦称“博奕论”。是研究对抗局势的数学理论。它是运用数学的方法确定带有对抗性质问题的数学模型。并在已知竞争或对抗的各方全部可以采取的策略而不知它方如何决策的情况下，研究竞争或对抗的各方是否存在最合理的行动方案和如何找到最合理的方案。一个对策问题必须具备局中人、策略及结局三要素。依照不同的原则可以把对策问题划分为不同的类型： 按局中人数可分为二人对策和多人对策； 按策略来划分可分为有限对策 （各方的策略个数有限） 和无限对策； 按一局得失之和来划分可分为零和对策与非零和对策； 按局中人有无合作分为合作对策与非合作对策，按其数学模型来划分可分为矩阵对策、连续对策、微分对策、阵地对策，等等。在各类对策模型中，二人零和有限对策占有重要地位，目前，对二人零和有限对策的理论研究及求解方法都比较完整，而其它对策模型的研究还处于发展阶段，二人零和有限对策的理论是研究其他对策模型的基础。描述、分析对策现象的方法有支付矩阵法、对策树法等等。

对策论

game theory

对策论game theory

亦称“博弈论”、“竞赛论”。(1) 运用数学理论研究有利害冲突的各方在竞争性的活动中自己取胜的最优策略的理论和方法。是应用数学的分支学科，也是运筹学的分支学科。主要研究公式化了的激励结构的相互作用，研究具有斗争或竞争性质的现象。在生物学、经济学、国际关系学、计算机科学、政治学、军事战略和其他很多学科都有广泛的应用。(2) 以博弈情境为比喻，探讨个体面临抉择时如何考虑得多失少以实现最优化决策的心理学研究。