复摆fubai

一个简谐振动的理想模型。任何一个能绕水平固定轴在竖直平面内摆动的刚体（轴线不过重心），当不计一切阻尼，摆角极小(一般小于5°)时，此振动系统称为复摆，又称物理摆。在振动过程中，复摆只受到重力和水平光滑轴对它的支持力的作用，重力对转轴的力矩是回复力矩。如图示，以m表示刚体质量，h表示重心到转轴的距离，I表示刚体对转轴的转动惯量。选取逆时针为角坐标θ的正方向，则角坐标θ表示刚体相对于平衡位置的角位移。由于θ极小，sinθ≈θ，刚体受到指向平衡位置的力矩为M=-^mghθ。式中θ用弧度为单位。根据转动定律可得复摆振动的动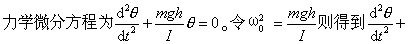
ω₂₀θ=0，其解为复摆的运动学方程θ=θ₀cos(ω0t+ᵠ)，表明复摆作简谐振动。复摆的振幅θ0是最大角位移的绝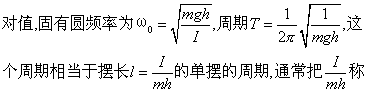为复摆的等值摆长。复摆可看作摆长为等值摆长l、摆锤质量为m的等价单摆。在刚体上延长OC到P点使OP=I/m_h，则点P称为复摆的振动中心，而点O称为悬置中心。对于任何复摆来说，其悬置中心和振动中心是可以互换的，即复摆绕O点的振动周期与绕P点的振动周期相等，所以称O、P两点相互共轭。根据这一原理制成的可倒摆，可用来精确地测定各地域的重力加速度。在许多计时仪器中都要用到复摆，如在摆钟中，控制时针运走快慢的钟摆，就是一个复摆。

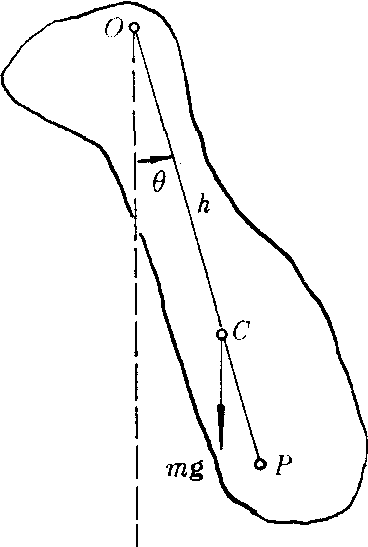
复摆

又称“物理摆”。任何一种能绕水平固定轴旋转并在重力作用下处于稳定平衡态的物体，如钟摆。在重力作用下摆动时，如果振幅很小，则其振动周期为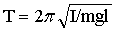：；式中I是物体对轴线的转动惯量，m是物体的质量，1是物体的重心与轴线间的垂直距离。

复摆

compound pendulum