复合函数的求导法则
复合函数的求导法则fuhe hanshu de qiudaofaze
若函数u=φ(x)在点x存在导数φ ′ (x),函数y=f (u)在其对应点u也存在导数f′ (u),则复合函数y=f [φ (x)] 在点x也可导,且有法则
{f [φ (x)]}′ =f′ (u)φ ′ (x) =f′ [φ (x)]φ ′ (x)
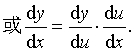
本法则通常称为链式法则,可推广到有限次复合的情形。如对于三次复合的情形,若y=f (u),u=φ (x),x=g (t)都可导,则 (f {φ [g (t)]})′ =f′(u) φ ′ (x) g′ (t)。
复合函数求导法则的作用是将某些复杂函数的导数化为几个更基本的函数的导数的乘积,以便简化运算。运用该法则的关键在于正确地分析函数的复合过程。
例 求 y=sin2 (2x+π/3)的导数。
| 解 设 |
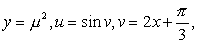
| 则 |
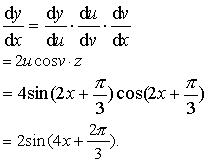
☚ 反函数的求导法则 由参数方程所确定的函数的求导法则 ☛
- 闿明是什么意思
- 闿朗是什么意思
- 闿泽是什么意思
- 闿爽是什么意思
- 闿疏是什么意思
- 闿置是什么意思
- 闿门是什么意思
- 闿阐是什么意思
- 闿阖是什么意思
- 闿阳是什么意思
- 阀是什么意思
- 阀值是什么意思
- 阀尔是什么意思
- 阀门是什么意思
- 阀门产品手册是什么意思
- 阀门厂是什么意思
- 阀门技术手册是什么意思
- 阀门选用手册是什么意思
- 阀阅是什么意思
- 阀阅名家是什么意思
- 阀阅舞射柳蕤丸记是什么意思
- 阁是什么意思
- 阁上是什么意思
- 阁上青藜是什么意思
- 阁下是什么意思
- 阁下令史是什么意思
- 阁下(称呼)是什么意思
- 阁不住是什么意思
- 阁丞是什么意思
- 阁中咨访是什么意思
- 阁中帝子今何在,槛外长江空自流。是什么意思
- 阁事是什么意思
- 阁仔是什么意思
- 阁住是什么意思
- 阁儿是什么意思
- 阁免是什么意思
- 阁内都督部曲是什么意思
- 阁几是什么意思
- 阁前是什么意思
- 阁前双槿是什么意思
- 阁前迎春花是什么意思
- 阁压是什么意思
- 阁厢是什么意思
- 阁台是什么意思
- 阁号是什么意思
- 阁向西山收拾紫,花从内苑借将红。是什么意思
- 阁员是什么意思
- 阁员大臣是什么意思
- 阁啰是什么意思
- 阁嘘青蜃,楼啄彩虹,飞盖蹴鳌背。是什么意思
- 阁堂前是什么意思
- 阁夜是什么意思
- 阁子是什么意思
- 阁子头石窟是什么意思
- 阁子头石窟造像是什么意思
- 阁学是什么意思
- 阁学士是什么意思
- 阁室是什么意思
- 阁岩是什么意思
- 阁峰是什么意思