域和代数扩域yu he daishukuoyu

作为代数结构.域是数域概念的推广，几乎适合数域的所有基本性质，域中元素可以不是数，而为任意对象.
至少含有两个元素的集合F，有两个代数运算加法与乘法.加法、乘法都适合交换律、结合律，且适合乘法对加法的分配律；有元0和1，分别适合a+0=a,1·a=a，对所有a∈F成立；并且，方程a+x=b,a·x=b(a ≠0)，对任何a,b，在F中有解.则F称为域.
所有数域都是域.p为素数，则剩余类环Z_p是域.F={0,1}对以下加乘运算做成域.实际是Z₂.

+	0	1	·	0	1
0	0	1	0	0	0
1	1	0	1	0	1

若域F的子集E对F的运算做成域，则E称为F的一个子域，而F称为E为一个扩域.
例如，有理数域Q是实数域R的一个子域；也是复

数域C的一个子域；Q也是

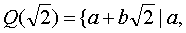
b∈Q}

的子域.并且，

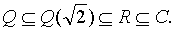
若元a适合

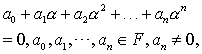
则a称为域F上的一个代数元.

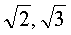
都是Q上的代数元.它们分别适合

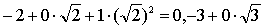
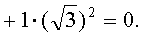
若域F中不存在a0,a1,a2，…，an(an≠0)使

则a称为F上的超越元.
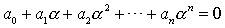
常用对数中的e，圆周率π都是Q上的超越元，通常称为超越数.
若域F的扩域E的每个元都是F上的代数元，则E称为F的一个代数扩域.
例如，Q()是Q的代数扩域.而R不是Q的代数扩域.但C是R的代数扩域.