圆锥曲线的切线yuanzhuiquxian de qiexian

经过圆锥曲线Ax²+Bxy+Cy²+Dx+Ey+F=0上一点P (x₁,y₁)的切线方程是

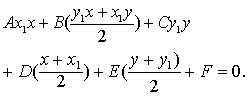
证 设Q(x₁+△x,y₁+△y)是曲线上和P (x,y)点邻近的点，则
Ax²₁+Bx₁y₁+Cy²₁+Dx₁+Ey₁+F=0
A(x₁+△x)²+B(x₁+△x)(y₁+△y)+C(y+△y)²+D(x₁+△x)+E(y₁+△y)+F=0
两式相减，并整理，得

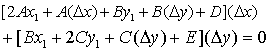
由此可得

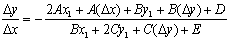
两边取极限，可得曲线在P点的斜率

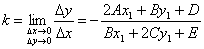
故经过P点的切线方程是

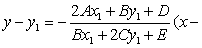
x1),

整理可得

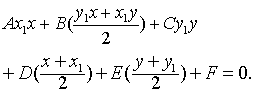
已知曲线上一点P的坐标(x₁,y₁)，可按下述变形规则，将曲线方程直接改写成以P点为切点的切线方程：
❶将x2和y²变形为x₁x和y₁y;
❷将xy变形为(y₁x+x₁y)/2;
❸将x和y变形为(x+x₁)/2和(y+y₁)/2;
❹常数项不变.
求经过不在圆锥曲线上的已知点的切线方程，不能用上述的变形规则.
经过圆或椭圆外部一点，双曲线内部(不包含双曲线两焦点的平面区域，如满足x²/a₂-y²/b²<1的点集)一点，抛物线外部(不包含抛物线焦点的平面区域，如满足y²>2px的点集)一点，都可以分别作圆或椭圆，双曲线，抛物线的两条切线，求切线方程的常用方法有两种.
方法1 设已知点为P₀(x₀,y₀)，切点为P₁(x₁,y₁)，按上述变形规则写出过P₁点的切线方程；将P₀点坐标代入此切线方程，得出关于x₁和y₁的方程.
由于P₁点在曲线上，将P₁点坐标代入曲线方程，得出另一个关于x₁和y₁的方程.
解方程组求出切点坐标，便可写出切线方程.
方法2 设所求的过P₀ (x₀,y₀)点的切线方程是y-y₀＝k(x-x₀)，其中斜率k是待定系数.将此切线方程和曲线方程联立，组成方程组.
消去一元，化为关于x(或y)的一元二次方程，令其判别式⊿=0，解出k值，便可写出切线方程.
应用方法2时，应注意不要遗漏斜率不存在(垂直于X轴)的切线方程.
若已知点在圆或椭圆的内部，双曲线的外部(包含双曲线焦点的平面区域，如满足x²/a²-y²/b²>1的点集)，抛物线的内部(包含抛物线焦点的平面区域，如满足y²<2px的点集)，则不能做圆或椭圆，双曲线，抛物线的切线.