圆锥
汉《九章算术·商功》
【评】此圆锥体积公式基于周三径一:V=l2h。其中l,h分别为下周长,高。
按:此术圆锥下周以为方锥下方。方锥下方令自乘,以高乘之,合三而一,得大方锥之积[“方锥”原本作“锥方”,依李潢改]。大锥方之积合十二圆矣。今求一圆,复合十二除之,故令三乘十二得三十六而连除。
于徽术,当下周自乘,以高乘之,又以二十五乘之,九百四十二而一。
《九章算术·商功》三国魏·刘徽注
【评】此为刘徽所记载的对圆锥公式的证明及刘徽用π≈157/50对公式的修正。其中用到圆锥与以该圆锥底周长为底边的方锥体积之比等于1 ∶ 12的原理,当源于《九章算术》成书时代,亦为祖暅之原理的滥觞。
又,此术亦用周三径一之率。假令以三除周,得径。若不尽,通分内子,即为径之积分。令自乘,以高乘之,为三方锥之积分。母自相乘得九,为法。又当三而一,约方锥之积。从方锥中求圆锥之积,亦犹方幂求圆幂,乃当三乘之,四而一,[原本此下衍“方锥”二字,依戴震删],得圆锥[原本讹作“幂”,依戴震校正]之积。前求方锥〔原本脱“锥”字,钱宝琮补〕积乃合三而一,今求圆锥之积,复合三乘之。二母既同,故相准折。惟以四乘分母九,得三十六而连除,圆锥之积。
《九章算术·商功》三国魏·刘徽注
圆锥比于方锥,亦二百分之一百五十七。命径自乘者,亦当以一百五十七乘之,六百而一。其说如圆亭也。
《九章算术·商功》三国魏·刘徽注
【评】在“委粟术”中,《九章算术》又提出了以底径和高求圆
锥体积的公式V=d2h。刘徽以π≈ 157/50将其修正成V=d2h。证明中刘徽用到了圆锥与其外切方锥体积之比为π∶4的原理。
圆锥
《九章算术·方田》三国魏·刘徽注
[注]①见,读xian,见幂,侧面积。
【评】这里刘徽提出了正确的圆锥侧面积公式,并利用圆锥侧面积:方锥侧面积=π∶4的原理论证了它的正确性,考虑圆锥表面积,在中国古代不多见。
圆锥yuánzhuī
直角三角形以其任意一条直角边为轴,旋转一周所形成的立体
△ ~体。
★圆规 圆弧 圆圈 圆形 圆舞曲 圆周率 圆珠笔
★方圆 桂圆 汤圆 团圆 滚瓜溜圆 花好月圆 破镜重圆 字正腔圆
圆锥yuán zhuī
直角三角形以夹直角的任意一边为轴旋转一周所成的立体。1610年,利玛窦在《理法器撮要》中称圆锥为“员锥”。后来在邓玉函和王徵合译的《奇器图说》(1634年)中,又称“尖圆”。“圆锥”这词出现在后,如1859年艾约瑟译《重学》卷六:“一率,圆锥全质。”1873年丁韪良等《中西闻见录》第1号:“地月之体,皆半向日而生明,半背日而生长影,因皆小于日,故长影若圆锥然。”
圆锥yuanzhui
用不经过顶点且垂直于轴的一个平面去截圆锥面,截面和圆锥面所围成的几何体叫做直圆锥,简称圆锥.
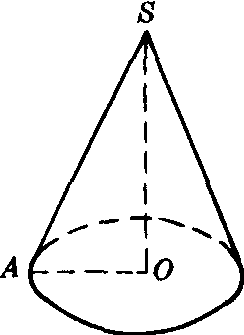
圆锥也可以看成是一个直角三角形SOA绕它的一条直角边SO旋转一周形成的旋转体(如图).SO所在的直线叫做圆锥的轴;直角三角形的斜边SA叫做圆锥的母线;由母线旋转所成的圆锥面叫做圆锥的侧面;直角三角形的另一条直角边OA旋转而成的圆面叫做圆锥的底面;圆锥顶点到底面的距离叫做圆锥的高.
圆锥一般可用它的顶点和底面圆心两个字母来表示,如图中的圆锥,可记作圆锥SO.
圆锥Yuanzhui
一个直角三角形,以它的一条直角边为轴, 旋转360°所成的旋转体, 如图就是直角形AOS绕它的一条直角边SO旋转一周形成的旋转体。SO所在的直线叫做圆锥的轴; 直角三角形斜边SA叫做圆锥的母线; 由母线旋转所成的圆锥面叫做圆锥的侧面; 直角三角形的另一条直角边AO旋转而成的圆面叫做圆锥的底面; 圆锥顶点到底面的距离叫做圆锥的高。圆锥一般可用它的顶点和底面圆心两个字母来表示,如图中的圆锥,可记作圆锥SO。圆锥有以下一些性质:
❶圆锥的底面是一个圆面, 它垂直于圆锥的轴。
❷圆锥的轴经过顶点和底面的圆心。顶点和底面圆心的连线等于圆锥的高。
❸圆锥的母线都经过顶点并且相等。
❹圆锥的各条母线与轴的夹角都相等。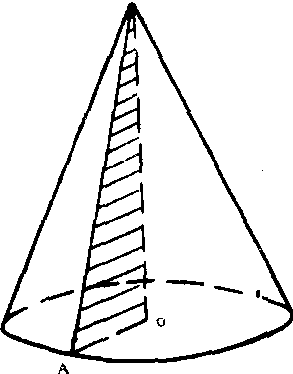
圆锥
cone
- 放浪形骸地狂饮是什么意思
- 放浪无拘是什么意思
- 放浪无羁是什么意思
- 放浪江湖是什么意思
- 放浪潇洒是什么意思
- 放浪牛是什么意思
- 放浪轻浮是什么意思
- 放浪,放荡是什么意思
- 放浮屎是什么意思
- 放海灯是什么意思
- 放淤是什么意思
- 放淤固堤是什么意思
- 放淤种稻是什么意思
- 放淫是什么意思
- 放淫距诐是什么意思
- 放清光万道,入户穿窗,皎皎昏蒙普济。是什么意思
- 放港是什么意思
- 放港的是什么意思
- 放游是什么意思
- 放游畜是什么意思
- 放湖鸭是什么意思
- 放溜是什么意思
- 放溢是什么意思
- 放滚水是什么意思
- 放滥是什么意思
- 放漂是什么意思
- 放漫是什么意思
- 放潘是什么意思
- 放火是什么意思
- 放火三日是什么意思
- 放火又一头放水是什么意思
- 放火号是什么意思
- 放火孟良盗骨殖是什么意思
- 放火容易救火难是什么意思
- 放火必毕是什么意思
- 放火杀人是什么意思
- 放火案件是什么意思
- 放火案件侦查是什么意思
- 放火炮是什么意思
- 放火烧山是什么意思
- 放火烧山野的草木是什么意思
- 放火烧荒是什么意思
- 放火父是什么意思
- 放火癞司是什么意思
- 放火示威,拥众自卫是什么意思
- 放火罪是什么意思
- 放火罪未遂是什么意思
- 放火自烧身是什么意思
- 放火诈骗案是什么意思
- 放灯是什么意思
- 放炕是什么意思
- 放炮是什么意思
- 放炮仔是什么意思
- 放炮仗是什么意思
- 放炮的是什么意思
- 放点是什么意思
- 放点心学是什么意思
- 放烂药是什么意思
- 放烟幕是什么意思
- 放烟幕弹是什么意思