四色问题sise wenti

图论的一个著名猜想.画地图时，希望相邻（即有共同边界）的国家和地区能使用不同的颜色，这种着色称为正常着色.1852年格色里在实际工作中发现，仅用四种颜色对地图进行正常着色，可使任两相邻的区域能着不同的颜色.这就是著名的四色猜想，也称为四色问题.
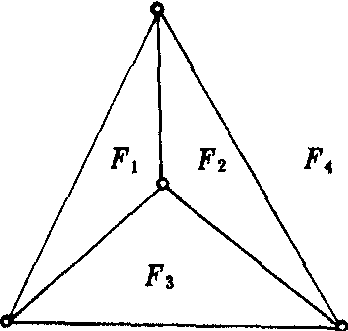
给地图正常着色至少需用四种颜色.这可从例子中看到：四个区域彼此相邻，按正常着色的定义，需用四种颜色.

1879年肯普给出了四色猜想的第一个“证明”.到1890年，希伍德发现肯普的“证明”是错的；但他证明了用五种颜色可以给任何平面图正常着色.
一百多年来，四色猜想一直成为许多数学家感兴趣而又没有解决的图论难题。1976年阿佩尔、黑肯、柯奇发表了借用电子计算机所作的证明，费机时1200小时，但一些数学家不满意这一结果.

四色问题sise wenti

1852年，英国青年学生弗朗西斯·葛斯里(Francis Guthrie)问他的哥哥弗雷德里克 ·葛斯里(Frederick Guthrie)提出了一个问题：世界上的地图看来都可以只用4种颜色来染色， 以使每两个有共同边界的国家有不同的颜色。能否在数学上证明这一结论？在这里“有共同边界”是指沿一条边界线相邻而不是在一个点相邻的国家，否则，一幅地图上的国家如果看起来像是一张馅饼分成的楔形块， 那么有多少国家就需要多少种颜色(图1)。“国家”是指一个连通区域，因为，如果一个国家可以由不止一个区域组成，而这些区域是隔离的，那就不难作出一幅5国地图的例子， 其中每个国家都与其余四国中每一国相邻(图2)。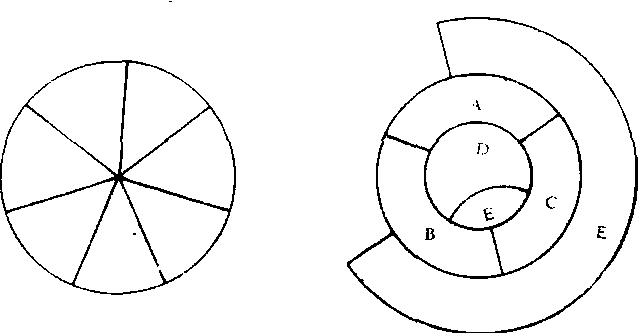

图1 图2

弗雷德里克无法回答弗朗西斯提出的问题， 就去请教他的老师， 数学家德·摩根 (De Morgan)。德·摩根无法证明，就写信求教于哈密顿(Hamilton, W.R.), 后者也没有办法。据传说， 早在1840年， 德国数学家莫比乌斯(Mobius, A.F.)就曾提出过这一问题。
弗·葛斯里和德·摩根肯定认识到， 可以画出一幅4国地图，使得每个国家都同其余3国相邻，这样一幅地图需要4种颜色， 因而三色猜想不成立， 也就是说， 要对所有地图染色， 3种颜色是不够的。(图3)。

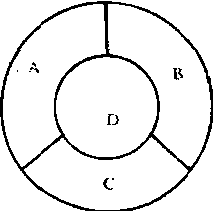
图3

德·摩根证明： 不可能有5个国家处于这样一种位置， 使得其中每一个都与其余四个相邻。这就使他相信，决不需要5种颜色，因而四色猜想一定是正确的，但是，证明地图上不可能存在5个彼此相邻的国家，并不等于证明了四色猜想，只要看一个简单的例子就够了：我们完全可以作出一幅地图，其中没有3个以上的国家彼此相邻， 却需要4种颜色 (图4)。

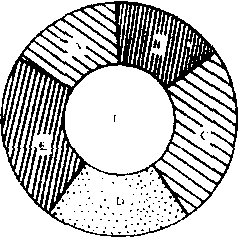
图4

1878年， 英国数学家凯莱(Cayley, A.)由于既不能证明也不能推翻四色猜想， 便把问题提交给伦敦数学会。从此，这一猜想在世界各国数学界广泛流传， 成为近代最著名的未解决的数学问题之一。
1879年，美国数学家肯普(Kempe, A. B.)给出了这一猜想的第一个 “证明”， 但1890年希伍德(Heawood, P. J.)发现了其中一个难以补救的错误，并证明若将四色猜想改为五色猜想， 结论是对的。此后，他继续不断地研究这一问题达60年以上。在此期间， 其他许多优秀数学家也为证明四色猜想付出了艰苦的努力，还发生了不少有趣的故事(参见“闵科夫斯基”)。应该指出的是，肯普的 “证明”虽然不成立，却包含了许多有价值的基本思想，给后人以极大的启发。
本世纪30年代人们发现：在数学中存在着这样一些定理，它们的陈述既简短又明确，但是其最短的证明也长得难以在适当的时间里写出来。50年代人们开始怀疑四色猜想就属于这一类命题，但是，寻找一个优美的数学证明的努力仍在继续着。到70年代初，许多四色问题专家对于找到一个简短的证明以解决四色问题已经完全悲观了，这个问题自从100多年前提出之后，受到很多关注，试用过许多方法，尽管某些方法在其他数学领域中产生了重要的结果， 却没有一种方法能证明四色猜想。
出人意料的是， 1976年， 美国数学家阿佩尔(Appel, K.)和哈肯 (Haken, W.) 与计算机科学家柯奇 (Koch, J.)合作， 用电子计算机证明了四色猜想，轰动了整个数学界。但是，为了完成这一证明，竟需要当时的大型计算机工作1200多个小时，人工根本无法验证。何况后来不断有人指出，阿佩尔等人的程序中有一些错误，他们也不断地在调整程序，改正错误。因此，这个计算机证明不能为数学家普遍接受。一些数学家惊呼：计算机进入了数学，数学的优美结束了！实际上，即使这个证明完全正确，从数学家的一般价值观来看，也只能说“四色猜想”的结论正确(因此可以改称之为“四色定理”)，并且可以用有限步数学推理予以证明 (虽然这个 “有限”之大是令人难以想象的)，但是一个相对简短的证明无论如何是必要的。因此，一方面，数学家们仍在努力探求着四色定理的简短证明，另一方面，由四色定理的计算机证明，也引起了人们对数学的本质、能力、方法等问题的思考，必将对数学的发展产生深远的影响。可以说，四色定理的计算机证明，不仅不是一个著名数学问题的结束， 而且标志着数学中一系列重大问题的开始。

四色问题

拓扑学中的一个问题。能否用四种颜色区别地图上的区域，使相邻的两个区域颜色不同。1976年美国数学家阿佩哈尔、哈肯和考西利用计算机证明了四色定理，即4种颜色可满足要求。

四色问题

拓朴学中的一个问题。在地图上要把所有的地区按照海洋和陆地的不同国属，用种种颜色加以区别，使相邻的两个地区有不同的颜色。如只用四种颜色是否能满足此要求的问题。这个问题据说是1840年由德国数学家麦比乌斯首先提出，1850年有个叫格色里的人曾就此问题询问英国数学家德·摩根从而引起人们的注意。数学家们花了一个多世纪的努力始终没有彻底解决这个问题。直到1976年，才由美国数学家阿佩尔、黑肯利用电子计算机，花费了1200小时，证明这一猜想可以解决。