可重复的组合ke chongfu de zuhe
从n个不同的元素里,每次取出m个元素,允许所取的每一个元素重复出现1,2,………,m次,不管怎样的顺序并成一组,叫做从n个元素中每次取出m个可重复的组合,其中m
例如,从A= {a1,a2,a3} 的三个元素中,每次取两个,不重复的组合为: a1a2,a1a2,a2a3,组合数为C32=3 (个); 可重复的组合为: a1a1,a1a2,a1a3,a2a2,a2as,a3a3,组合数为6 (个),用H32表示可重复的组合数,即: 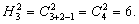
可重复组合的模型为:设有带号码1,2,………,n的n种球,每种都有足够多的个数 (也就是可重复),在这一堆球中,任意取出m个 (m可以大于n),不计它们的次序,组成一组,则其不同组合的数目为: Hnm =Cn+m-1m。
上述模型也可表述为:设袋中有带号码1,2,………,n的球各一个,在这n个球中任取一个,记下其号码后,放回袋中; 然后再取一个,同样记下号码后,放回袋中;………;依次重复m次,一共记下m个号码。不计它们的次序,归成为一组,则其不同组合的数目为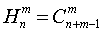 , 有时把可重复的组合数记作
, 有时把可重复的组合数记作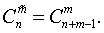
一般地,有如下定理:
在集合A= {a1,a2,………,an} 中,每次取m个元素的可重复的组合数为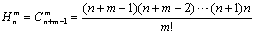
证 先将Hnm个所有重复组合中所含元素都按足码先小后大的顺序加以排列 (因为组合与元素的排列顺序无关,这样加以排列对于各个组合没有影响),足码最小的元素放在最左边,足码愈大的愈放在右边,足码相同的邻接。为了明确起见,不妨以一个组合为例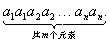
再将各元素下标依次加上0,1,2,………,(m-1)中的一个,使得上述组合成为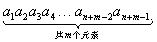
在这个组合中,m个元素变得都不相同,且下标的最小数字为1,下标的最大数字由n变为n+m-1,因此,它就成为从n+(m-1)个不同元素里每次取m个元素不重复组合中的一种组合。对所有组合都如此处理,因而都变为由a1到an+(m-1)的n+ (m-1)个不同元素里每次取m个元素的不重复的组合,反之,将由a1到an+(m-1)的n+ (m-1) 个元素每次取m个的不重复的组合每一个,先依其足码大小次序将每个元素排列,再将各足码的下标依次减去0,1,2,………,(m-1)中的一个,则所有不重复的组合都变为上述有重复的组合,因此,由n个不同元素中,每次取m个元素的重复组合数,等于由相应的n+(m-1)个不同元素中,每次取m个的不重复的组合数,即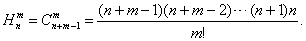
- 甜盘是什么意思
- 甜睡是什么意思
- 甜石榴是什么意思
- 甜磂磂是什么意思
- 甜秆是什么意思
- 甜秆子是什么意思
- 甜秆秆是什么意思
- 甜秆高粱是什么意思
- 甜种是什么意思
- 甜秫秸是什么意思
- 甜秫稭是什么意思
- 甜竹是什么意思
- 甜竿是什么意思
- 甜箩是什么意思
- 甜米拉西是什么意思
- 甜米米是什么意思
- 甜米酒是什么意思
- 甜米黍是什么意思
- 甜粄是什么意思
- 甜粑解围是什么意思
- 甜粥是什么意思
- 甜粼粼是什么意思
- 甜粿是什么意思
- 甜糕是什么意思
- 甜糖抹在鼻头上——只闻得香却舔不着是什么意思
- 甜糖抹在鼻子上——舐不着是什么意思
- 甜糟是什么意思
- 甜细细的是什么意思
- 甜绝是什么意思
- 甜美是什么意思
- 甜美动听的、讨好人的话是什么意思
- 甜美动听的话是什么意思
- 甜美圆润是什么意思
- 甜美爽口是什么意思
- 甜美的味道是什么意思
- 甜美的果实是什么意思
- 甜美的槟榔是什么意思
- 甜美的泉水是什么意思
- 甜美的露是什么意思
- 甜美纯净是什么意思
- 甜美芬香是什么意思
- 甜美芳香是什么意思
- 甜羹是什么意思
- 甜老是什么意思
- 甜者是什么意思
- 甜而光亮是什么意思
- 甜而爽口是什么意思
- 甜而苦是什么意思
- 甜腥是什么意思
- 甜腥腥是什么意思
- 甜腻是什么意思
- 甜腻腻是什么意思
- 甜芦粟是什么意思
- 甜芦黍是什么意思
- 甜花笑面是什么意思
- 甜花肉香是什么意思
- 甜花酸是什么意思
- 甜苣是什么意思
- 甜苣奶子是什么意思
- 甜苣苣[taytay]是什么意思