反馈系统分析

反馈系统是指一种具有反馈联系的自动控制系统，生物调节系统和生物随动系统都是这种反馈系统(参见“生物控制系统”条)。为了研究反馈系统的动态品质，控制理论已发展了一些常用的分析方法。
传递函数 它是动态系统输出与输入量之间的定量表达式。系统的传递函数可通过理论推导或实验方法得到。对生物系统来说，一般只能通过实验求得。以血压调节系统为例，如以停止人工呼吸5秒作为输入，通过动物试验可以得到动脉压变化的曲线，如图1所示。这一过程可近似用二阶微分方程来表示。因输入作用时间相对很短，可看作是一个脉冲量，可用A(δ)来表示，而血压用X来表示时，则有方程式ω²Ẍ+2ξẊ+x=A(δ)，其中，X、X分别
表示X的二阶和一阶导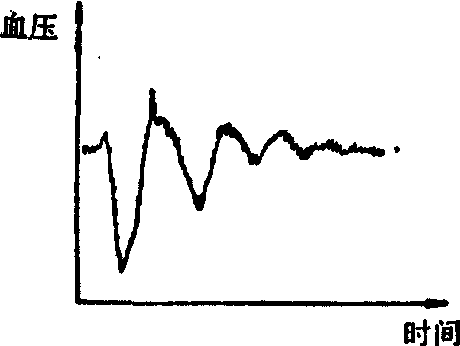

数，ξ和ω为表示不同个
体特性的参数。ξ和ω
不同，动脉压输出波形
也不同，由此可对系统
进行定量研究，如已应
用于研究药物和针刺对
血压调节系统的影响。
图1 血压对停止呼吸的响应
在拉氏变换以后，上述微分方程可化为代数方程，即ω2S2X(s)+2ξωX(s)+X(s)=A(s)，式中s为拉氏变换算符，X(s),A(s)为X和A经变换后的结果，它们都是s的函数。输入A(s)与输出X(s)之比是所研究的血压系
统的传递函数，其数学关系为
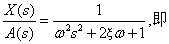
传递函数为零初始条件下，输出量（响应函数）的拉氏变换与输入量（驱动函数）的拉氏变换之比。
传递函数属于“黑箱”表示方法，它表示了系统本身的特性，而与输入量或驱动函数无关。在用传递函数分析反馈系统时，可先将系统分解为容易确定其传递函数的典型环节。由于经过拉氏变换后，环节间的动态联系变为代数关系，因此，可从环节的传递函数经代数运算求出整个系统的传递函数。传递函数与输入函数的拉氏变换乘积，则为输出的拉氏变换，通过拉氏反变换即可求出输出随时间的变化，于是可求出不同输入下的系统的响应。在实际工作中，可由表中查出拉氏变换或拉氏反变换的结果。典型环节的传递函数很容易从其输入输出方程中
求出，例如惯性环节，其输出输入方程为
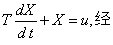
拉氏变换有TSX(s)+X(s)=(TS+1)X(s)=u(s)，则
其传递函数为
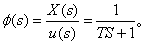
各种典型环节的传递函数如下。
❶惯性环节： 传递函
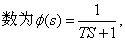
式中T为时间常数。惯性环节的阶
跃响应函数具有指数规律。很多生物反馈系统中都含有惯性环节；
❷积分环节：传递函数为φ(s)=1/TS。其阶跃响应为斜率等于1/T的直线；
❸微分环节： 传递函数为φ(s)=TS。在实际系统中阶跃响应函数具有尖脉冲形式；
❹比例环节：传递函数为一常数K。输出量的幅度与输入量的幅度成比例，比例常数为K;
❺二阶环节： 传递
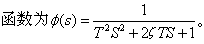
很多系统都可以分解
成由上述各典型环节组合而成的系统。例如血糖调节系统，如果考虑调节中最基本的因素，该系统的控制部分是由比例环节和微分环节并联构成的，对于因葡萄糖输入而引起的胰岛素响应特性，通常包含了快速分泌相和缓慢分泌相两个响应成分，其中快速分泌相是微分环节的响应特性，而缓慢分泌相则是比例环节的响应特性。
用传递函数表示系统的一个环节的特性，从其系统结构框图，很容易通过代数运算获得整个系统的传递函数。
❶串联：如环节W1(s)和环节W2(s)相串联，则总传递函数φ(s)为二环节传递函数之积，即φ(s)=W1(s)·W2(s);
❷并联：环节W₁(s)和环节W₂(s)相并联，其总传递函数φ(s)等于两者之和，即φ(s)=W1(s)+W2(s);
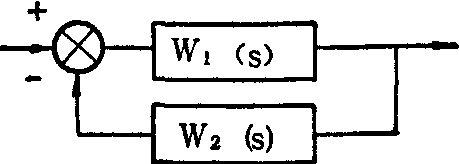
❸反馈：如图2所示反馈系统，系统闭环传递函数为φ(s)=
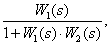
式中W₁(s)·W₂(s)又称为开环传递
函数。利用传递函数不
必求解微分方程就能分
析控制系统的性能，并
计算出系统在各种输入
时的动态特性。
图2 反馈系统
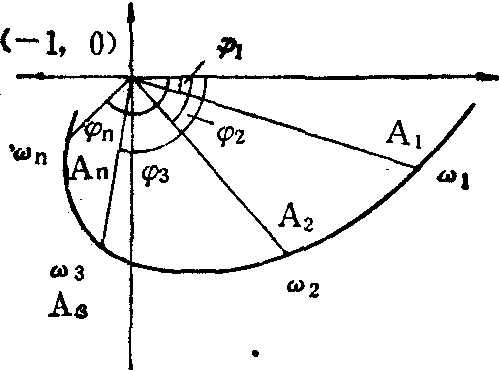
频率特性分析 系统对正弦波输入的响应称为频率响应。用一系列不同频率的正弦波信号输入到一个系统中，可以得到相应不同频率的输出。如果系统是线性的，那么输出为与输入频率相同的正弦波，但其幅值与相位不同。此幅值与相位的差别反映了系统的动态特征。将输出与输入幅值之比，以及两者的相位差作成以频率为函数的曲线，称为频率特性曲线。频率特性曲线可由传递函数中，用S=jω代换而得到。线性常系数系统中，传递函数与频率特性是相对应的。在生物系统研究中，大多数是用实验方法直接求出频率特性曲线，通过频率特性曲线可求出系统的传递函数，并进一步可以分析系统的稳定性。用极坐标绘制出的频率特性曲线称为乃氏图，用对数标尺分别绘出幅值和相位差与频率的关系，则称为对数频率特性。控制理论已建立了由开环系统的频率特性去确定系统闭环后是否稳定的准则，即开环系统的乃氏图如不包围(-1,0)点时，闭环系统是稳定的。因此，通过实验得到乃氏图以及影响乃氏图的因素，就可分析各因素对闭环稳定性的影响，确定生物系统不稳定的原因。生物系统在正常情况下是闭环的。要做开环频率特性试验常常要经手术开环，并用特殊的输入信号装置。在实验中，常采用等幅正弦波输入，这样可在不同频率下得到输
出的幅值及与输入的相位差，可得到如下数据：

频率ω	ω1	ω2	ω3	……	ωn
幅值A	A1	A2	A3	……	An
相差φ	φ1	φ2	φ3	……	φn

由此表可绘出乃氏图，如图3所示。一例狗脑中枢缺血反应开环频率特性如图4所示。在压力为30mmHg时，乃氏图通过(-1,0)点，因此闭环系统是不稳定的，这与用人工方法造成脑血流压力减到30mmHg时可引起血压的振荡（三级波）的结果相符合。开环频率特性试验方
法，已应用于研究
肾上腺皮质激素、
血压调节系统、呼
吸控制系统、瞳孔
控制系统等，通过
实验求出相应系统
的传递函数，并分
析这些闭环系统的
稳定性。
图3 频率特性曲线

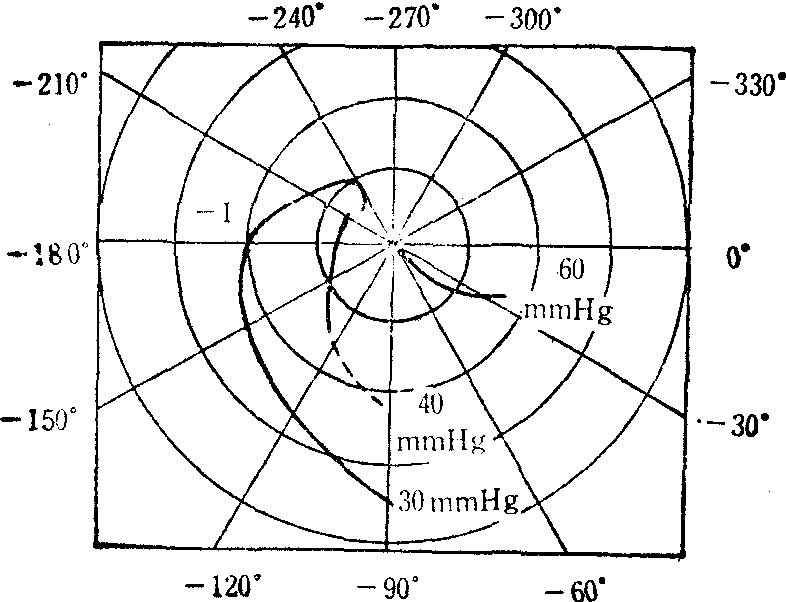
图4 脑缺血回路频率特性曲线

上述分析方法，适用于线性系统，即由线性常系数微分方程描述的动态系统。一般讲，线性系统仅是生物系统的近似的描述；实际生物系统中有非线性环节存在，如神经元的阈值，各种感受器输入与输出间的对数关系等。对于非线性系统需要用更复杂的数学方法进行分析。