反演变换fanyan bianhuan

一种几何变换.设平面内有一定圆，圆心为O，半径为r.若某一变换把平面内异于点O的任意一点A，变为直线OA上一点A′，并且|OA|·|OA′|=r2，则称为这种变换为平面内关于圆O的反演变换，圆O称为反演基圆（简称反演圆），点O为反演中心或反演极，半径r称为反演半径或反演幂.点A和点A′叫做关于圆O的互逆点或反点.
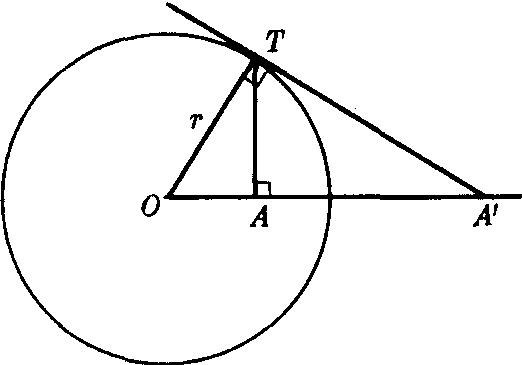
用下面方法可以作出一点A关于⊙O的反演点A′:❶当点A在圆内时（如图），过点A作OA的垂线交圆于点T，过点T作⊙O的切线交OA的延长线于点A′，利用直角三角形内直角顶点在斜边上射影的性质，可以证明|OA|·|OA′|=r²，所以点A与点A′互为反点；
❷当点A在圆外时，按上述相反的顺序，可以作出点A的反点A′;
❸当点A在圆上时，由定义可知它的反点就是点A本身.

若把圆心的反演点规定为无穷远点，则平面上的反演变换也是平面的一一变换.
若图形M上各点经过反演变换得到图形M′，则称图形M′是图形M的反形，或称图形M与M′互为反形.