利用容斥原理计数Liyong rongchi yuanli jishu

是把需要计数的大集合分为若干子集， 对子集分别计数，并根据容斥原理（参见容斥原理条），去除重复计数的数目，得到大集合的计数。这种计数方法的关键在于正确理解和使用容斥原理。
例1:从1到1 000的整数中，不能被5整除也不能被7整除的数有多少？
解：先考虑从1到1 000，能被5或7整除的整数集合的元素个数，设此集合为A，令集合B表示A中能被5整除的数构成的子集，而集合C表示A中能被7整除的数构成的子集， 那么|B|=1 000/5的整数部分=200, 而|C|=1 000/7的整数部分=142, 这里|B|、|C|分别表示集合B、C中的元素个数，以下同，根据容斥原理：|A|=|B|+|C|-|Bnc|，而|Bnc|=1 000/35的整数部分=28, 故|A|=200+142-28=314，即1到1 000中，能被5或7整除的数有314个，从而从1到1 000的整数中，不被5整除也不被7整除的数有 1 000-314=686个。
注意， 在计算|A|的时候， 必须减去|Bnc|, 因为在计算|B|和|C|时|Bnc|被重复计数。
例2（首届华罗庚金杯赛初赛试题）:每边长为10厘米的正方形纸片，正中间挖了一个正方形的洞，成为一个宽度是1厘米的方框， 把五个这样的方框放在桌面上，成为下图的图案，问桌面上被这些方框盖住的那部分面积是多少平方厘米。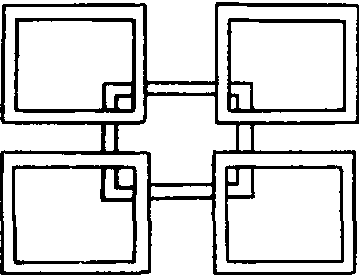
解： 首先要计算出 一个方框的面积。方框的宽度是1厘米， 因此被挖去的正方形边长是8厘米， 方框面积=100平方厘米-64平方厘米=36平方厘米。如果5个这样的方框互不相交地放在桌子上， 那么
盖住面积是180平方厘米(5×36)，在图示情形下，桌面上有8小块(1平方厘米)被两个方框共同盖住，因此如图图案的面积是180-8=172平方厘米。