利润最大化lì rùn zuì dà huàмаксимизция прбыли

利润最大化profit maximization

经济利润可以被定义成厂商的收益与成本之差。对厂商行为的多数经济分析是基于这样一个假定：即最大化其利润。即厂商选择行动(a1，…，an)，以便最大化R(a1，…，an)-C(a1，…，an)。实现利润最大化的基本条件有两个。(1)边际收益要等于边际成本，即MR=MC。因为如果边际收益大于边际成本，增大该活动的水平是有利可图的；而如果边际收益小于边际成本，则减少该活动的水平是合算的。只有当两者相等时，才可能实现利润最大化。如厂商在决定它的产出水平时，应选择这样的产量：在此水平上，如果再增加一单位产出的生产，只能获得等于它的边际生产成本的边际收益。厂商需要做出的另一项决定是要确定需要雇佣多少某一特定的要素，比如说劳动。利润最大化的这个基本条件告诉我们，厂商应雇佣的劳动量应使得再多雇佣一单位劳动的边际收益等于雇佣那个额外劳动单位的边际成本。(2)MR’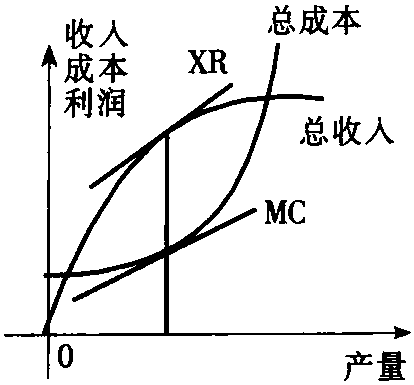*，它就是利润最大化的产量。在这一点上，两条曲线的斜率相等。总收入的斜率为边际收入MR，而总成本曲线的斜率为边际成本MC。因此利润最大化要求：MC=MR。

利润最大化Profit Maximization

企业经营的目标。必要条件是边际收益等于边际成本，即MR=MC；充分条件是利润函数的二阶导数小于零，即边际收益的变化率小于边际成本的变化率。可以将厂商的利润最大化转化为两种特殊情况：
❶当总成本给定，等价于收益最大化；当商品价格作为不变参数，等价于产量最大化。
❷当产量给定，价格是不变参数，其收益也给定，利润最大化等价于成本最小化。

利润最大化

生产者追求最大利润的行为。生产者把利润最大化作为自己追求的目标，这是微观经济学中的一个基本假定。利润是生产者的总收益减去总成本的差额。生产者的总收益、总成本和利润都与其产量相关，但是利润最大化并不等于产量最大化。因为在不同的产量水平上，总收益与总成本的变动量并不相同，因而利润水平也不相同。特别是当产量上升到一定水平后，总成本的增加将超过总收益的增加而使利润水平下降。因此，生产者需要确定在多大的产量水平上才能使利润达到最大化。现以横轴表示产量，纵轴表示收益、成本、利润的金额，图中给出三条曲线：总收益曲线、总成本曲线和利润曲线。
总收益曲线是表示生产者出售其产品的总收益与其产量之间相互关系的曲线。它表明，当产量为0时，总收益亦为0；随着产量的增加，总收益也增加；当产量超过一定水平后，由于规模不经济，总收益开始下降。总收益曲线的斜率是边际收益(以MR代表)。
总成本曲线是表示生产者的总成本与其产量之间相互关系的曲线。它表明，当产量为0时，由于有固定成本的存在，总成本大于0；随着产量的增加，总成本缓慢上升；而当产量超过一定水平后，企业规模的不经济使总成本迅速上升。总成本曲线的斜率是边际成本(以MC代表)。
利润曲线是表示生产者的利润与其产量之间相互关系的曲线。它表明，在产量水平较低时，利润为负，因为总收益不足以抵补固定成本和可变成本。这时边际收益大于边际成本，增加产量会使利润增加。随着产量的增加，利润上升，直到产量增加到一定水平(q^*)为止。这时边际收益等于边际成本(M R=M C)，也就是总收益曲线在A点的斜率与总成本曲线在B点的斜率相等。此时，总收益曲线与总成本曲线之间的垂直距离AB达到最大，即利润最大(利润曲线上的C点)。当产量超过这个水平(q^*)后，由于总成本的迅速上升，边际收益小于边际成本，使总收益曲线与总成本曲线之间的垂直距离缩小，即利润下降。因此利润最大化的产量水平是边际收益与边际成本相等时的产量水平。在完全竞争市场中，生产者按既定的价格(以P代表)出售其产品，生产者的边际收益等于其产品的市场价格，即M R=P。而生产者所选择的利润最大化的产量水平要求其边际成本等于边际收益，于是：

M C=M R=P

在利润最大化的产量下，生产者产品的边际成本等于其边际收益，并等于其市场价格，这一条件就是完全竞争市场中的“利润最大化法则”。

利润最大化profit maximization

传统微观经济学关于厂商行为的一个基本命题。通常认为，厂商从事各种决策经营活动的目的，是为了获取最大限度的利润。但也有一些经济学家不同意这种观点，认为厂商特别是现代大公司的经济动机并不仅限于追逐利润，甚至主要的不是为了利润。根据传统分析，利润最大化的一般条件是边际收益等于边际成本，即MR=MC。对此可以利用简单的数学方法来推导。令TR为总收益，TC为总成本，TP为总利润，便有TP=TR-TC; 将该式两端分别对产量求导，得(dTP)/(dQ)=(dTR)/(dQ)-(dTC)/(dQ)；由于当一阶导数为零时函数有极值，故最大利润条件应为dTP/(dQ)=(dTR)/(dQ)-(dTC)/(dQ)=0，即(dTR)/(dQ)=(dTC)/(dQ)。这里的dTR/(dQ)就是边际收益，(dTC)/(dQ)就是边际成本，因此上述条件得证。
对于上述条件，也可以用图形来说明。
两图描绘的是，随着销售量增加价格保持不变时总利润的变化情况。在图1中，边际收益曲线与边际成本曲线相交于E点，此时产量为Q_e，总利润为矩形阴影面积，显然，此时的面积代表了各种可能的利润水平中的最大利润。图2的图形更明白地证实了这一点，在对应E点的Q_e产量上，总收益曲线与总成本曲线的斜率相等，这时它们之间的垂直距离最大，从而总利润达于最大值。

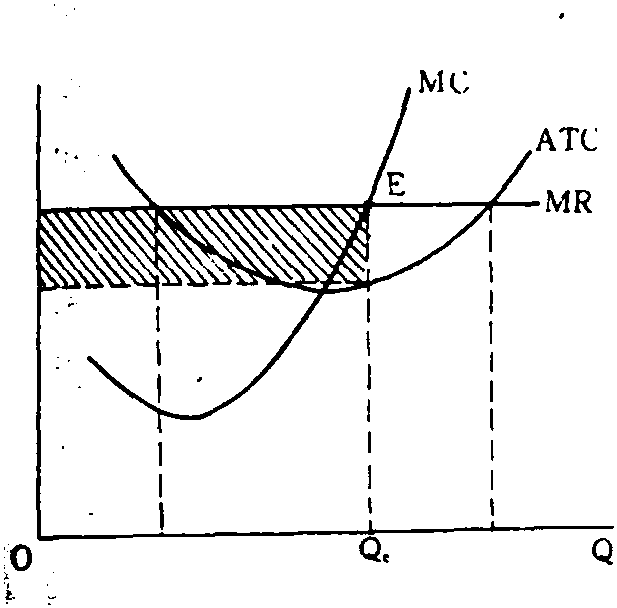
图 1

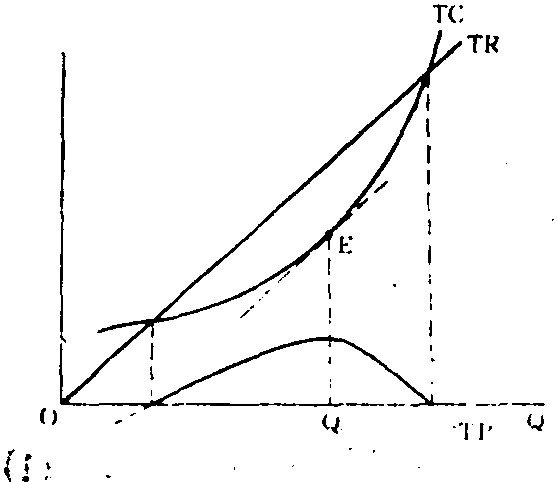
图 2

因此，边际收益等于边际成本作为最大利润均衡的一般条件，在逻辑上是毫无疑问的。

利润最大化profit maximization

利润最大化是西方经济学中有关厂商行为的基本假定，利润(π)是厂商的惟一的目标函数，它认为厂商所追求的目标就是使其利润达到最大化。这里，利润被定义为厂商收益(TR)与总成本(TC)之差。利润最大化就是要使总收益与总成本的余额最大。西方经济学假定，当产量增加到一定限度，便会出现边际收益(MR)递减和边际成本(MC)递增。因而，利润最大化不等于产量最大化。一般来讲，dπ/dQ=MRMC，显然，在零产量与最大产量之间存在使得利润最大化的一点，即dπ/dQ=0的那一点。此时MR=MC。显然，如果MCMR，可以通过减少产量来增大利润。也可以将利润函数写成价格（产品和生产要素价格）和数量（投入量与产出量）的形式，这样得到的利润最大化一阶条件为：每一种生产要素投入的边际产品的价值等于该要素的价格；二阶条件为：在厂商利润最大化的这一点上，生产函数的二阶导数矩阵是半负定的，即要求厂商的生产函数在利润最大化点的邻域内是凹的。