函数的图象hanshu de tuxiang

设函数y=f(x)的定义域为D.如果取D中每一个x的值及对应的y=f(x)而得到的数对(x,y)作为点的坐标，在坐标平面上的点集F={(x,y)|y=f(x),x∈D}就叫做函数y=f(x)的图象.例如函数y=kx+b(k≠0)是过(0,b)点的一条直线；函数y=x2的图象是以Y轴为对称轴，原点为顶点的抛物线.

函数的图象Hanshu de tuxiang

在坐标平面上直观地表示函数的一个图形。设y是x的函数： y=f (x)。我们可以把自变量x的值和与它对应的函数y的值作为平面的一个点的坐标， 在直角坐标系内描出一个点来，所有这些点的集合，叫做这个函数的图象。当我们知道了一个函数的解析表达式以后， 可以通过列表、描点、连线三个步骤来画出图象。
例： 画出函数y=x²的图象。
❶列表： 在x的取值范围内取一些值， 算出y的值。

x	…	-2	-1	0	1	2	…
y	…	4	1	0	1	4	…

❷根据表中的每一组对应值， 在直角坐标系内描点。

❸用光滑的曲线，按自变量从小到大的顺序，把所描的点连接起来， 就得到函数y=x²的图象。
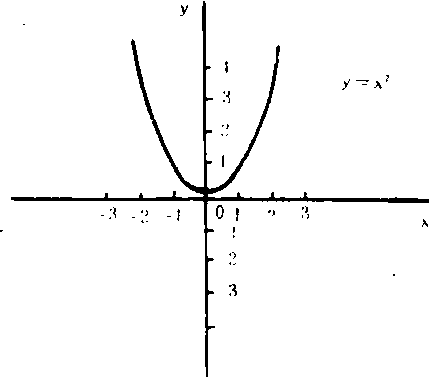
这种画图象的方法叫做描点法。这样画出的图象一般是近似的、部分的。如果描出的点多一些， 画出的图象会更精确一些。