几何平均数
指n个观察值的乘积的n次方根,常用xG表示。若用n表示观察值的个数,用x1,x2,…,xn表示观察值,则xG=![]() =n
=n![]() xi;若给出的是已经经过整理的频数分布表,用x1,x2,…,xk表示可能的观察值(或组中值),用fi表示观察到的xi的个数,i=1,2,…,k,又记n=f1+f2+…+fk=
xi;若给出的是已经经过整理的频数分布表,用x1,x2,…,xk表示可能的观察值(或组中值),用fi表示观察到的xi的个数,i=1,2,…,k,又记n=f1+f2+…+fk=![]() fi,则xG=
fi,则xG=![]() =n
=n![]() xfii。当x1,x2,…,xk表示组中值时所求得的xG是一个近似值。常被应用于测验分析统计中。
xfii。当x1,x2,…,xk表示组中值时所求得的xG是一个近似值。常被应用于测验分析统计中。
几何平均数geometric mean
一群变量值的积用个数开方所得的结果。通常用来表示现象的平均发展速度或计算某种变动比率的平均数。计算公式为:
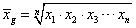
 g为几何平均数;xi代表变量值;n代表变量值的个数。在分组数列的情况下,计算公式为:
g为几何平均数;xi代表变量值;n代表变量值的个数。在分组数列的情况下,计算公式为: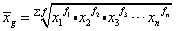
几何平均数jihe pingjun shu
当数据呈几何级数增加时,应以几何平均数作为这些数据平均数的代表值。例如,计算阅读能力、理解能力等的平均进步率和某些现象的平均发展速度,要用几何平均数法。几何平均数用MG表示,公式为:
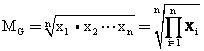
几何平均数Jihe pingjunshu
已知n个正数a1,a2,……,an。把这n个正数相乘,再把乘积开n次方,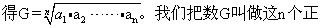
数a1,a2,……,an的几何平均数。例如,一个长方形的边长分别为a和b。如果想做一正方形,使它的面积等于长方形的面积ab,那么它的边长就是a和b这两个数的几何平均数 (如图)。这个几何问题可以看作几何平均数的来源。
(如图)。这个几何问题可以看作几何平均数的来源。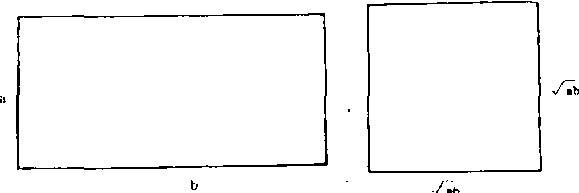
几何平均数
在统计中常用来表示现象的平均发展速度,是n个变量值连乘积的n次根。分为简单平均和加权平均,常用对数来计算。
几何平均数Geometric Average
n个变量值连乘积的n次方根。多用于计算平均比率和平均速度,如平均利率、平均发展速度、平均合格率等。几何平均数主要特点为:
❶受极端值的影响较算术平均数小;
❷如果变量值有负值,计算出的几何平均数就会成为负数或虚数;
❸仅适用于具有等比或近似等比关系的数据;
❹其对数是各变量值对数的算术平均数。
几何平均数
用n个变量值的连乘积开n次方来计算平均数的一种形式。它是计算平均比率和平均速度最适用的一种方法。这是因为几何平均数的数学性质与社会现象发展的平均比率和平均速度形成的客观过程相一致。凡是变量的连乘积等于总比率或总速度的现象都可以适用几何平均数计算平均比率或平均速度。几何平均数分为简单几何平均数和加权几何平均数两种。简单几何平均数的计算公式是:
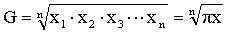
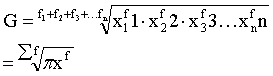
几何平均数
n个变量值连乘积的n次方根。有简单平均与加权平均之分。
简单几何平均数计算公式:
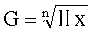
式中,G代表几何平均数; x代表各变量值;n为变量个数; Ⅱ为连乘符号。
加权几何平均数计算公式:
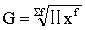
式中,∑f代表次数(或权数) 总和; f为每个变量值的次数 (或要数)。
几何平均数geometric average
n个变量值连乘积的n次方根。有简单平均与加权平均之分。
简单几何平均数计算公式:
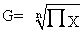
式中,G代表几何平均数;x代表各变量值;n为变量个数;Ⅱ为连乘符号。
加权几何平均数计算公式:

式中,∑f代表次数(或权数)总和;f为每个变量值的次数(或要数)。
几何平均数
有简单几何平均数和加权几何平均数两种。简单几何平均数是n个变量值连乘积的n次方根,适用于未分组的变量数列。加权几何平均数适用于已分组的变量数列。
几何平均数
几个变量值连乘开几次方根。是平均数的一种。由于几何平均数是计算平均比率或平均速度方面较适合的一种方法,因此几何平均数常用于计算平均发展速度。其计算公式为:
式中: 为几何平均数, x为变量值,n为变量值的项数,π为连乘符号。在实际计算工作中,由于变量个 数较多,通常要应用对数来进行计算,故又称“对数平均数”。将上式两边各取对数,则上式演变为: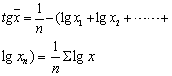
从变为对数的公式中可以看出,几何平均数的对数就是各变量值的对数的算术平均数。求出几何平均数的对数后,再由对数找出真数,即为几何平均数。几何平均数的特点是:
❶受极端数值的影响,较算术平均数和调和平均数小。
❷平均的数列中不能有一项为0; 如数列中有负值,计算的几何平均数就会成为负数或虚数。
❸使用范围较窄。
几何平均数
亦称“几何平均”。用n个变量值的连乘积开n次方来计算平均数的一种方法。其计算公式为。

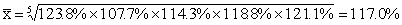
几何平均数geometric mean
几个变量值的连乘积的几次正方根, 以MG表示。在统计中,有许多统计量数系列是按几何级数来变异的,这种量数系列就叫做几何系列。几何平均数就是几何系列的中心量数。其计算公式为:
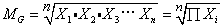
式中X1,X2,X3…Xn为各量数的取值;П是连乘的符号;n为总次数。如遇n较大,需要多次开方,计算较繁难时,通常可用对数来计算,上列公式可改写为:
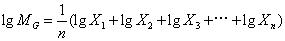
如在一组量数中,仅知初期数量,末期数量及期限,求各期平均发展速度时,表示平均发展速度的几何平均数等于各个环比发展速度的连乘积的n次正方根,即
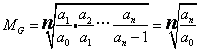
式中a0为最初水平,an为最末水平,a1/a0,a2/a1等为环比发展速度,n为环比发展速度的个数。
几何平均数geometric mean
集中量数的一种。n个观察值连乘积的n次方根。用Mg表示。主要用于衡量环比、速度以及数值非常巨大等类型数据的集中趋势。
- 中国新闻图史是什么意思
- 中国新闻工作者职业道德准则是什么意思
- 中国新闻界网络媒体公约是什么意思
- 中国明朝土地立法是什么意思
- 中国明朝水利立法是什么意思
- 中国明朝环境保护立法是什么意思
- 中国春秋土地立法是什么意思
- 中国春秋战国水利立法是什么意思
- 中国晋朝土地立法是什么意思
- 中国最大的方剂学着作是什么意思
- 中国最早介绍曲酒的专着是什么意思
- 中国最早介绍笔墨纸砚的专着是什么意思
- 中国最早全面介绍工农业技术的着作是什么意思
- 中国最早的伤科专着是什么意思
- 中国最早的佛教着作是什么意思
- 中国最早的修辞学专着是什么意思
- 中国最早的光学专着是什么意思
- 中国最早的古钱币着作是什么意思
- 中国最早的地理专着是什么意思
- 中国最早的天文历算着作是什么意思
- 中国最早的天文学专着是什么意思
- 中国最早的妇产科专着是什么意思
- 中国最早的建筑学着作是什么意思
- 中国最早的戏曲史着作是什么意思
- 中国最早的戏曲理论着作是什么意思
- 中国最早的戏曲论着是什么意思
- 中国最早的教育学专着是什么意思
- 中国最早的文物集成专着是什么意思
- 中国最早的有关花卉画技法的理论专着是什么意思
- 中国最早的植物学着作是什么意思
- 中国最早的法医学专着是什么意思
- 中国最早的法学着作是什么意思
- 中国最早的漆工专着是什么意思
- 中国最早的潮汐史专着是什么意思
- 中国最早的甲骨文专着是什么意思
- 中国最早的科学家传记着作是什么意思
- 中国最早的笑话专着是什么意思
- 中国最早的经济地理着作是什么意思
- 中国最早的脉学专着是什么意思
- 中国最早的药物学专着是什么意思
- 中国最早的营养学着作是什么意思
- 中国最早的语法专着是什么意思
- 中国最早的速记法着作是什么意思
- 中国最早的造园专着是什么意思
- 中国最早着录版本的书目是什么意思
- 中国最早研究文言虚字的专着是什么意思
- 中国最早研究甲骨文的专着是什么意思
- 中国最早给风力分级的专着是什么意思
- 中国最早记载物候的着作是什么意思
- 中国最早论述表演艺术经验的专着是什么意思
- 中国最早评论书法的专着是什么意思
- 中国最重要的数学专着是什么意思
- 中国服务质量大写真是什么意思
- 中国机动车排气年度检测立法是什么意思
- 中国机动车燃料生产控制立法是什么意思
- 中国机动车船排气限制立法是什么意思
- 中国机动车辆排气标准立法是什么意思
- 中国杜绝出口羊绒掺杂使假立法是什么意思
- 中国标准文献分类法是什么意思
- 中国梨木虱是什么意思