关于直线的对称变换的性质guanyu zhixian deduicheng bianhuan de xingzhi

如下：
❶任意一点P与它的像点P′到对称轴上任意一点L的距离都相等，即|PL|=|P′L|，并且对称轴是连结P,P′的线段PP′的垂直平分线；
❷任意一条直线与它的对称直线或者与对称轴平行，且与对称轴距离相等，或者相交于对称轴上同一点；
❸任意一个图形经过对称变换后与原图形合同（全等），但方向相反.
两个关于直线的对称变换的乘积不是对称变换，所以平面上对称变换的全体不构成群(如图1).但是平面上任何移动都可以用不多于三次的对称变换得到.例如，图2中△ABC到△A′B′C′是平面上一个任意移动.连结AA′，以AA′的垂直平分线l1为轴作对称变换，得△A′B₁C₁，连结C₁C′，以C₁C′的垂直平分线l₂为轴作对称变换，得△A′B₂C′.最后以A′C′为对称轴作对称变换，即可得△A′B′C′.

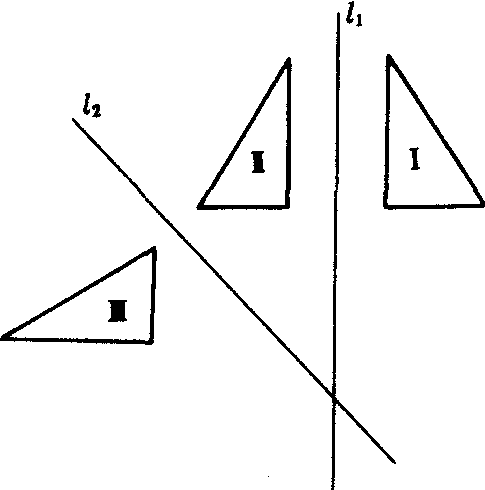
图1

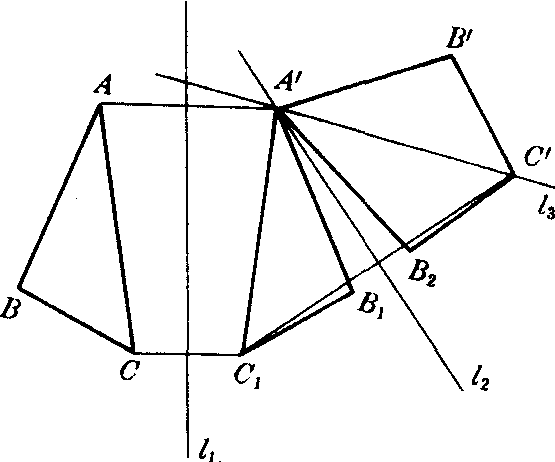
图2

在对称变换下，对称轴上的点都是对称变换的不动点，对称轴及通过每对对称点的直线都是对称变换下的不动直线.