信号的相关技术

相关函数说明信号之间的关联程度，包括互相关函数和自相关函数两种。
互相关函数 两个信号x(t)、y(t)的互相关函数在一定条件下可定义为：

式中R_xy(τ)为信号y(t)平移时间τ时和x(t)信号的互相关函数。如果使τ由小到大取不同值，分别求对应于每一τ值的R_xy(τ)，就能得出R_xy(τ)随τ变化的全貌。互相关函数说明两信号波形相似的程度。如果当τ=τ0时互相关值R_xy(τ0)达到极大，则y(t)移动τ0后，y(t+τ₀)和x(t)波形最相似；Rxy(τ₀)愈大，两者波形愈相似。如果x(t)和y(t)完全无关，则它们的互相关函数将恒等于零。
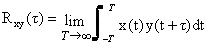
互相关技术可用来估计两个相似信号间的延迟时间，设y(t)是x(t)的延迟，则将y(t)左移至R_xy(τ₀)达到极大时的τ0为两信号间的延迟时间(见图1)。例如，从微血管的显微电视图象中测量红细胞运动速度时，可在电视图象上沿血管的上游和下游各设置一个窗口，取出各窗口内的光密度信号，再求这两个信号间的互相关函数，由相关函数极大值所对应的延迟τ₀和两窗口间的距离d₀，可求得红细胞的运动速度。

自相关函数 如果x(t) 和y(t)是同一个信号，则相应的相关函数称为自相关函数，可定义为：它说明同一信号相隔时间τ的不同时刻取值间的关联程度。

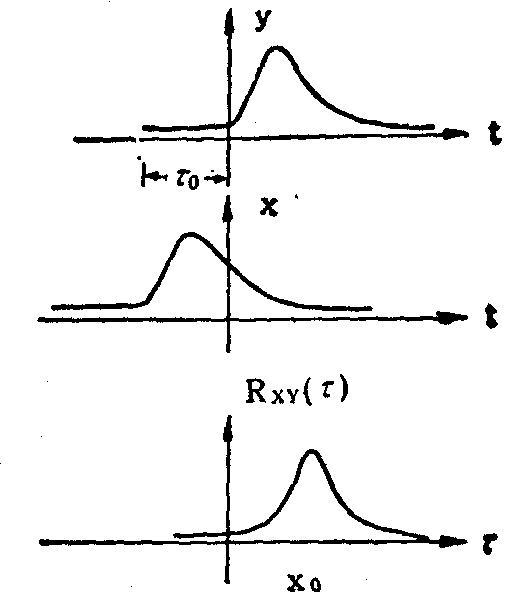
图1 利用互相关技术
估计信号的延迟

自相关函数的特性
❶对于一般的非周期信号，Rx(τ)随τ的加大而减小。信号上相隔时间愈近的两点，取值的关联程度愈大；相隔时间愈远的两点，取值的关联程度愈小[图2(a)、(b)]。随机性愈强的信号，不同时刻取值的关联程度愈小，其Rx(τ)随τ增加而下降得愈快。若信号的自相关函数Rx(τ)只在τ=0时有值，而在τ≠0时恒等于零，则此信号称为白噪声〔图2(d)〕。白噪声在任意两个时刻的取值总是不相关的，其随机性最强；
❷周期性信号的自相关函数也具有周期性，其周期与信号的周期相等〔图2(c)〕；
❸自相关函数的富氏变换是信号的功率谱(参见“信号的谱分析”条)。

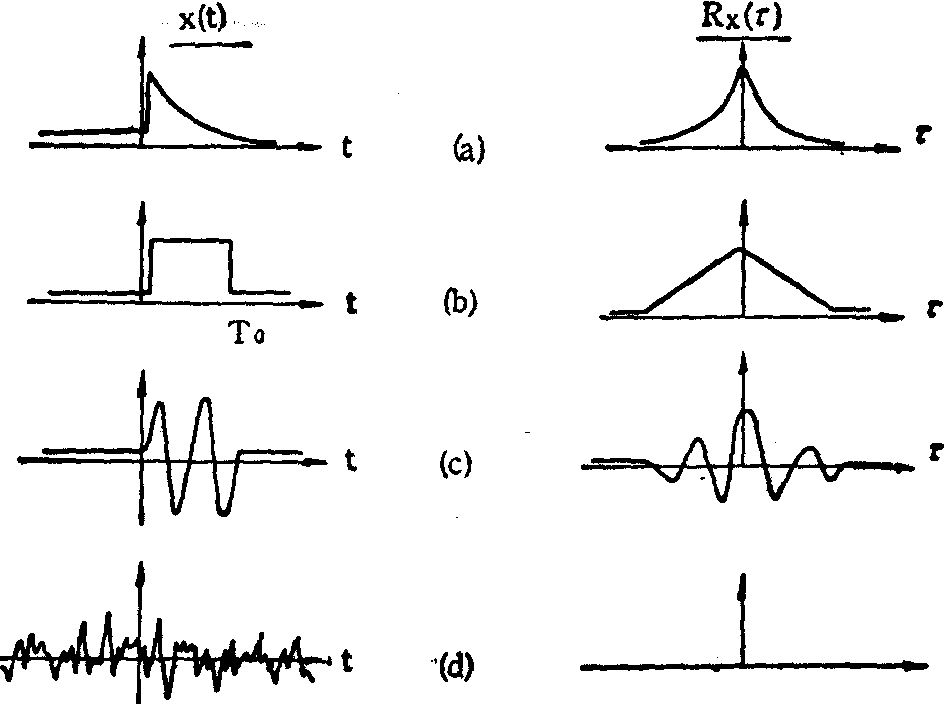
图2 自相关函数的特性

相关函数的性质可用于从观察值中检测信号是否存在。
❶当观察值x(t)由信号S(t)和噪声n(t)相加而成，信号和噪声不相关，且信号的波形已知时，可对S(t)和x(t)作互相关处理。由于x(t)=S(t)+n(t),R_xS(τ)=RS(τ)+R_sn(τ),R_Sn(τ)=0，则有R_xS(τ)=R_s(τ)，即S(t)和x(t)间的互相关函数等于信号的自相关函数。于是根据R_xS(τ)值便可判断信号是否存在。例如在超声医学中，常将这一原理用于检测超声脉冲射向生物体后引起的反射回声；
❷如果信号和噪声不相关，其波形并非已知，而其周期性已知时，可对观察值x(t)作自相关处理。由于R_x(τ)=R_s(τ)+Rn(τ)，而一般情况下噪声的自相关函数R_n(τ)随τ的加大而迅速减小，周期信号的自相关函数R_s(τ)却是周期性的，因此只要τ足够大，Rn(τ)便可忽略，此时R_x(τ)≃R_S(τ)，并随τ加大而周期重复。于是根据R_x(τ)值既可检测信号是否存在，又可以估计信号的周期。例如，通过对离体鼠肾血流信号作自相关处理后，可发现信号具有约15ms的周期振荡。