中国剩余定理

068 中国剩余定理

即孙子剩余定理。见32067孙子剩余定理。

中国剩余定理孙子定理Zhongguo Shengyudingli

关于求解同余式组的定理，是由我国古代数学家孙子发明的。我国古代的《孙子算经》中提出了如下问题：“今有物不知其数，三三数之剩二，五五数之剩三，七七数之剩二，问物几何？”。如果用同余式表达。设x为所求的物数， 那么问题可以被写成下面的形式： 解同余式组：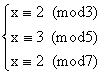
解上述的“物不知其数”问题，或较一般地解同余式组：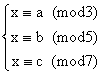
它的一般解式为x≡70a+21b+15c (mod105)。关于这个一般解法， 在明朝程大位的 《算法统宗》(1593) 里有以下歌诀：
三人同行七十稀，五树梅花廿一枝，七子团圆正半月，除百零五便得知。
这样，“物不知其数”问题的解是：以70乘以用3除所得的余数，以21乘以用5除所得的余数，以15乘以用7除所得的余数，全加起来，再减去105的倍数，即70×2+21×3+15×2=233，减去105的2倍，得23，这就是所求的物数。
中国剩余定理的一般形式如下：
如果m₁m₂，……m_k是两两互素的k(k≥2)个正整数， 令M=m₁m₂……m_k＝m₁M₁＝m₂M₂＝……=m_kM_k, 那么满足同余式组：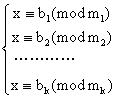
的整数解是
x≡b₁M'₁M₁+b₂M'₂M₂+……+b_kM'_kM_k(modM)，这里M'i是满足同余式M'_iM_i≡1(modm₁)
的正整数解， i=1, 2…， k。
例1:在上述“物不知其数问题中”，取m₁＝3, m₂＝5, m₃＝7, b₁＝a, b₂＝b, b₃＝c, 那么M=3×5×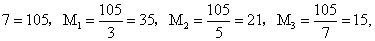为求M′₁, 注意到35≡2mod3, 70≡35×2≡2×2(mod3), 即70≡35×2≡1 (mod3), 可以取M′₁＝2，类似地可以得到M′₂＝1, M′₃＝1, 因此M′₁M₁＝70,M′₂M ₂＝21,M′₃M₃＝15同余式组x≡a (mod3), x≡b (mod5), x≡c (mod7) 的一般解是x≡70a+21b+15c (mod105)。
例2: 一个数除以5余3, 除以6余4, 除以7余1。求适合条件的最小自然数。此题是求适合下列同余式组的最小自然数x: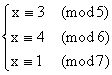
令m₁＝5, m₂＝6, m₃＝7, 则m₁, m₂, m₃两两互素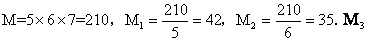，＝210/7=30。
❶42≡2mod5,3≡3(mod5)，因此126≡6≡1 (mod5), 取M′1=3。
❷35≡5 (mod6), 5≡5(mod6), 因此175≡25≡1(mod6)，取M′2=5。
❸30≡2(mod7), 4≡4 (mod7)，因此120≡8≡1(mod7)，取M′₃＝4。于是M′₁M₁＝126,M′₂M₂＝175, M′₃M₃＝120, 3×126+4×175+1×120=1198。x≡1198(mod210)是同余式组的一般解，其中1198-210×5=148为满足条件的最小自然数)。

中国剩余定理

见“孙子问题”。