万有引力定律wanyou yinli dinglu

物体（质点）间由=F它们的引力质量而引起的相互吸引力所遵循的规律。自然界中任何两个质点都以一定的力互相吸引着，这个力的方向沿着它们的连线，其大小与它们的质量乘积成正比，与它们之间的距离平方成反比，即F=Gm¹·m₂/r₂。式中m₁和m₂表示这两个质点的质量，r表示它们之间的距离，G是比例系数，称为万有引力常数，G=6.672 0×10-¹¹牛顿·米²/千克²。万有引力定律只适用于可以看作是质点的物体。若求任意的两个物体间的引力，则必须把每个物体分成很多小部分，每个小部分看成是一个质点，计算所有这些质点间的相互作用力。对于两个均匀球体，它们之间的引力可以直接用万有引力定律表示式计算，这时式中的γ表示两球球心间的距离。一个均匀球体对球外一个质点的引力也可以用同样公式计算，而γ是球心到质点的距离。原因在于球体是中心对称的，实际积分结果也确实如此。对两个相距不太远的非球形物体，例如两个60千克的人相距1米时，求他们之间的吸引力就不能简单地把两人质心间距作为γ代入公式来计算。由于万有引力常数G的数值非常小，所以一般质量不是很大的物体间的引力是很小的，可以忽略不计。上述例子中两人之间的吸引力的数量级是10^-7牛顿，相当于一粒砂子重量的万分之一或几百粒尘埃的重量。对于质量很大的天体之间，万有引力是很大的。例如太阳和地球之间的吸引力大约等于3.56×102²牛顿，这样大的力可以将直径为几千米的钢柱拉断。万有引力定律的建立经历了 一个过程。开普勒定律发表后，很多科学家都在研究行星为什么要沿开普勒轨道运行。1679年前后，英国科学家胡克(Hooke,1635～1703)、哈雷(Halley,1656～1742)、雷恩(Wren,1632～1723)等人，都按照圆形轨道由开普勒第三定律和惠更斯的向心力公式推导出太阳与行星之间存在的吸引力，是一种和距离平方成反比的力，但这种力为什么会形成椭圆轨道，他们没有能够从理论上得到证明。彻底解决这个问题的人是牛顿，他从研究月球绕地球运动入手，探索引力定律，不仅在观念上肯定了地球上的引力与天体间引力的同一性，并且在开普勒三定律基础上，运用自己的力学成就和微积分，从理论上证明了引力跟距离的平方成反比。牛顿由开始研究万有引力定律(1665年)，到最后发表在《自然哲学的数学原理》上(1686年)，一共花了21年时间。万有引力定律揭示了天体运动的规律，在天文学上和宇宙航行计算方面有着广泛的应用。它为实际的天文观测提供了一套计算方法，可以只凭少数观测资料，就能算出长周期运行的天体运动轨道，科学史上哈雷彗星、海王星、冥王星的发现，都是应用万有引力定律取得重大成就的例子。利用万有引力公式，开普勒第三定律等还可以计算太阳、地球等无法直接测量的天体的质量。牛顿还解释了月亮和太阳的万有引力引起的潮汐现象。他依据万有引力定律和其他力学定律，对地球两极呈扁平形状的原因和地轴复杂的运动，也成功地作了说明。

万有引力定律

牛顿1687年发现的关于物体间相互作用的一条定律。天体力学的理论基础。参见“物理”中的“万有引力定律”。

万有引力定律

对于万有引力的发现，许多科学家都做出了贡献。引力的概念古已有之，在古希腊哲学家亚里士多德看来，万物皆有它固定的位置，一旦离开原位它就要力争回到原位。石头落地就是因为石头要回到它原来的宇宙中心的位置。但这只是亚里士多德的没有任何根据的臆想。
著名天文学家尼古拉·哥白尼认为，引力是物质的一种集聚的趋向，物质在任何地点都会聚集成球状，而不一定是在宇宙中心，引力的中心在物质的球心。科尔切斯特的威廉·吉尔伯特在1600年提出磁力是维持太阳系运行的引力，他根据磁石实验，将地球视为一块磁石，引力就是地球这块大磁石对各种物体的磁力。法国17世纪的哲学家及数学家笛卡尔认为，物质之间并不存在可以穿越空间而起作用的引力，空间充满了物质，在石子落地的运动过程中石子并不是 “自由” 落体，石子落地是由于存在着包围地球表面的物质旋涡，也正是由于这种旋涡使天体沿圆周轨道运动而不是沿直线运动。荷兰的克利斯提安·惠更斯在1669年作了一项实验，他将碗里的水搅成旋涡，碗内的卵石都被冲到碗底的旋涡中心，惠更斯由此认为引力是包围着地球的 “以太” 的旋涡，这样似乎也证明了笛卡尔的说法。这一说法在当时产生了一定的影响，以致使人们不再重视引力的研究。英国皇家学会的干事罗伯特·虎克相信引力与吉尔伯特所研究的磁力类似，由于吉尔伯特已经证明了磁力的大小与物体间的距离的大小有关，因而虎克认为引力同样与物质间的距离有关。为了证明他的设想虎克做了一些实验，他把物体在深井中的重量与在地面及高山顶的重量进行比较，但他的实验并没有什么结果。
与此同时，牛顿也在对引力问题进行研究。据一些文献记载，牛顿对万有引力的猜测可以追溯到1666年，由于当时瘟疫流行，牛顿离开剑桥在沃尔斯索普隐居。据说牛顿在沃尔斯索普的果园里看到苹果落地，由此他想到引力问题，认识到使苹果落地的重力和使天体沿圆形闭合轨道运转的力，具有相同的性质。为了证明这一点，牛顿需要找出引力与距离的关系，并根据这一规律计算出月球的向心加速度，同时再根据月球圆周运动的速度计算出向心加速度。如果两种计算所得结果一致，那么就证实了他的设想。在计算过程中牛顿推导出了平方反比定律，即引力与距离的平方成反比。在计算月球的实际向心加速度时需要知道地球的半径，由于当时尚无地球半径的精确数值，因此计算结果产生了约为15%的偏差，这样牛顿只好将他的研究暂时搁置起来。也有人认为牛顿之所以没有马上发表他的计算是因为他当时还不知如何确定离地球较近的物体与地球的有效距离，不知应该用物体距地表的距离还是应该用距地心的距离。直到1685年，牛顿终于证明了地球对物体的吸引力相当于地球的全部质量集中于地心的一个质点。
1687年牛顿的 《自然哲学的数学原理》 用拉丁文出版，这部著作被公认为科技史上最伟大的著作。在这部著作中牛顿详细而系统地阐明了万有引力原理，并利用这一原理解释了天体的运动规律和海水的潮汐运动等现象，这部著作奠定了天文学和宇宙学的思想基础。在 《自然哲学的数学原理》 出版之前英国的物理学家虎克曾声明他是引力的平方反比定律的最先发现者，于是在书中加入一段声明，指出虎克也是平方反比定律的独立发现者之一。1693年在皇家学会的一次会议上虎克再次声明他是向心力定律和平方反比定律的第一个发现者，这时牛顿正在患病，恢复健康后牛顿才声明他在1666年就已发现了向心力定律和平方反比定律。事实上牛顿只是许多解决引力问题的科学家之一，这些科学家都同时并且独立为解决引力问题做出了贡献。

万有引力定律

对于万有引力的发现，许多科学家都做出了贡献。引力的概念古已有之，在古希腊哲学家亚里士多德看来，万物皆有它固定的位置，一旦离开原位它就要力争回到原位。石头落地就是因为石头要回到它原来的宇宙中心的位置。但这只是亚里士多德的没有任何根据的臆想。
著名天文学家尼古拉·哥白尼认为，引力是物质的一种集聚的趋向，物质在任何地点都会聚集成球状，而不一定是在宇宙中心，引力的中心在物质的球心。科尔切斯特的威廉·吉尔伯特在1600年提出磁力是维持太阳系运行的引力，他根据磁石实验，将地球视为一块磁石，引力就是地球这块大磁石对各种物体的磁力。法国17世纪的哲学家及数学家笛卡尔认为，物质之间并不存在可以穿越空间而起作用的引力，空间充满了物质，在石子落地的运动过程中石子并不是 “自由”落体，石子落地是由于存在着包围地球表面的物质旋涡，也正是由于这种旋涡使天体沿圆周轨道运动而不是沿直线运动。荷兰的克利斯提安·惠更斯在1669年作了一项实验，他将碗里的水搅成旋涡，碗内的卵石都被冲到碗底的旋涡中心，惠更斯由此认为引力是包围着地球的 “以太”的旋涡，这样似乎也证明了笛卡尔的说法。这一说法在当时产生了一定的影响，以致使人们不再重视引力的研究。英国皇家学会的干事罗伯特·虎克相信引力与吉尔伯特所研究的磁力类似，由于吉尔伯特已经证明了磁力的大小与物体间的距离的大小有关，因而虎克认为引力同样与物质间的距离有关。
为了证明他的设想虎克做了一些实验，他把物体在深井中的重量与在地面及高山顶的重量进行比较，但他的实验并没有什么结果。
与此同时，牛顿也在对引力问题进行研究。据一些文献记载，牛顿对万有引力的猜测可以追溯到1666年，由于当时瘟疫流行，牛顿离开剑桥在沃尔斯索普隐居。据说牛顿在沃尔斯索普的果园里看到苹果落地，由此他想到引力问题，认识到使苹果落地的重力和使天体沿圆形闭合轨道运转的力，具有相同的性质。为了证明这一点，牛顿需要找出引力与距离的关系，并根据这一规律计算出月球的向心加速度，同时再根据月球圆周运动的速度计算出向心加速度。如果两种计算所得结果一致，那么就证实了他的设想。在计算过程中牛顿推导出了平方反比定律，即引力与距离的平方成反比。在计算月球的实际向心加速度时需要知道地球的半径，由于当时尚无地球半径的精确数值，因此计算结果产生了约为15%的偏差，这样牛顿只好将他的研究暂时搁置起来。也有人认为牛顿之所以没有马上发表他的计算是因为他当时还不知如何确定离地球较近的物体与地球的有效距离，不知应该用物体距地表的距离还是应该用距地心的距离。直到1685年，牛顿终于证明了地球对物体的吸引力相当于地球的全部质量集中于地心的一个质点。
1687年牛顿的 《自然哲学的数学原理》用拉丁文出版，这部著作被公认为科技史上最伟大的著作。在这部著作中牛顿详细而系统地阐明了万有引力原理，并利用这一原理解释了天体的运动规律和海水的潮汐运动等现象，这部著作奠定了天文学和宇宙学的思想基础。在 《自然哲学的数学原理》出版之前，英国的物理学家虎克曾声明他是引力的平方反比定律的最先发现者，于是在书中加入一段声明，指出虎克也是平方反比定律的独立发现者之一。1693年在皇家学会的一次会议上，虎克再次声明他是向心力定律和平方反比定律的第一个发现者。这时牛顿正在患病，恢复健康后牛顿才声明他在1666年就已发现了向心力定律和平方反比定律。事实上牛顿只是许多解决引力问题的科学家之一，这些科学家都同时并且独立为解决引力问题做出了贡献。

万有引力定律

由牛顿发现的具有一定距离的两个物体之间的引力定律：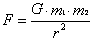

其中F为万有引力，G为万有引力恒量G=6.67×10-11牛，米²/千克²,m为两物体的质量，r为距离。这个定律适用于任何有一定距离的两个物体，但最主要的用途是揭示了天体之间的吸引力和运动情况，因而对天文学的发展起了重要作用。牛顿对万有引力的研究，首先是基于他本人和伽利略等科学家对地面上引力现象的研究，特别是对抛物体的研究。但牛顿大胆地把地球对高山上的物体的吸引与地球对月球的吸引相类比，然后又扩大到了宇宙所有天体。牛顿用微积分的方法证明了任何两个物体间的相互作用力，都可以用它们的质心之间的作用力来代替。这就把千差万别的地面物体或宇宙天体之间的相互作用，统统抽象为一个个质点的相互作用，因而使这一定律适用于一切物体。牛顿以超人的想像力发现万有引力定律的过程，在科学方法论上具有重要意义。他把复杂的对象抽象为质点进行科学研究，形成了一种典型的理想模型方法，对以后各门科学的发展都起到了巨大的作用。

万有引力定律

law of universal gravitation