F分布

如果随机变量X～χ²(n),Y～χ²(m)，且X与Y相互独立，则随机变量F=的分布称为具有自由度为n,m的F分布，记为F(n,m)。常被应用于测验分数统计中。

F分布

F分布是一种连续型分布，其重要性主要在于它是方差分析的基础。F是两个相互独立的x²变量分别除以各自的自由度后之比，即

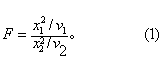
在实际应用时，F等于两样本方差或两均方之比。
密度函数及其图形 F分布的密度函数为

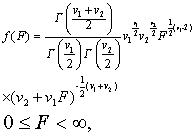
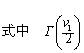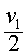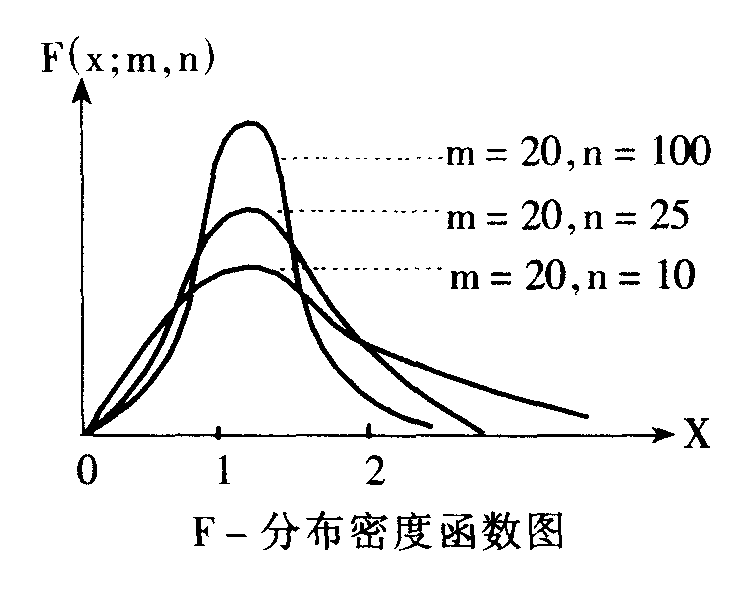
自由度v_t＝n₁-1,v₂＝n₂-1。为伽玛(gamma)函数在处的函数值，余
仿此，算法见条目“x²分布”。已知v1与v₂就能绘出F分布的图形，如图1。

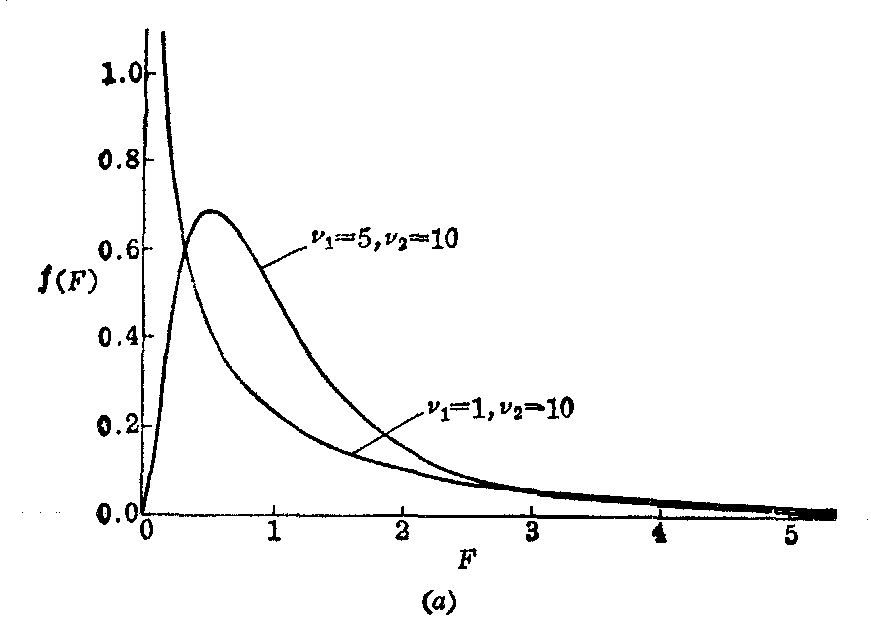
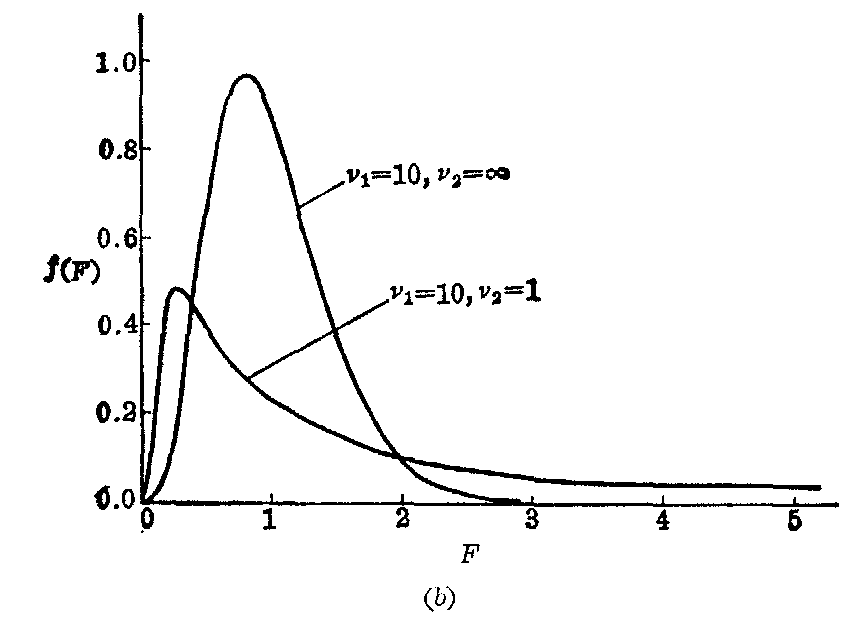
图1 不同自由度时的F分布曲线

F分布的分布函数为

式中f(F)为式(2)的密度函数，P(F) 的几何意义是F分布曲线下从0到某给定F值的面积，如图2(α)。
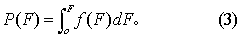
F分布的分位数 当v1、v₂确定后，F分布曲线下，右侧尾部的面积P为指定值α时，横轴上相应的界值F，记作Fα(v₁,v₂)，如图2(b)，这就是F分布的分位数，此值有F界值表(如表1及表2)可查。作F检验时，先求得观察样本的统计量F值后，按v₁及v₂可由表1或表2查得P值的大小。

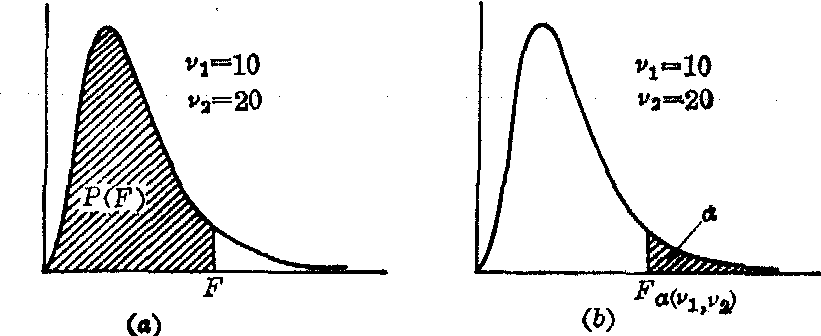
图2 F分布曲线下的面积

表1 F界值表，用于方差齐性检验，仅给出了双侧P=0.05(相当于单侧0.025)的分位数。因为方差齐性检验本是双侧检验，按理P值应为两端尾部面积之和，但在此检验中，规定较大方差作为分子，较小的作为分母，故F值不会小于1，这样，检验水准为0.05时，只需列出右端尾部面积为0.025的分位数。表2 F界值表，用于方差分析，表内数值为单侧P=0.05与P=0.01的分位数。

表1 F分布的分位数表(F界值表)
(方差齐性检验用，P=0.05)

v2(较小 均方的自 由 度	v1（较大均方的自由度）
	2	4	6	8	10	12	15	20	30	∞
2 3 4 5	39.00 16.04 10.65 8.43	39.25 15.10 9.60 7.39	39.33 14.73 9.20 6.98	39.37 14.54 8.98 6.76	39.40 14.42 8.84 6.62	39.41 14.34 8.75 6.52	39.43 14.25 8.66 6.43	39.45 14.17 8.56 6.33	39.46 14.08 8.46 6.23	39.50 13.90 8.26 6.02
6 7 8 9 10	7.26 6.54 6.06 5.71 5.46	6.23 5.52 5.05 4.72 4.47	5.82 5.12 4.65 4.32 4.07	5.60 4.90 4.43 4.10 3.85	5.46 4.76 4.30 3.96 3.72	5.37 4.67 4.20 3.87 3.62	5.27 4.57 4.10 3.77 3.52	5.17 4.47 4.00 3.67 3.42	5.07 4.36 3.89 3.56 3.31	4.85 4.14 3.67 3.33 3.08
12 15 20 30 ∞	5.10 4.77 4.46 4.18 3.69	4.12 3.80 3.51 3.25 2.79	3.73 3.41 3.13 2.87 2.41	3.51 3.20 2.91 2.65 2.19	3.37 3.06 2.77 2.51 2.05	3.28 2.96 2.68 2.41 1.94	3.18 2.86 2.57 2.31 1.83	3.07 2.76 2.46 2.20 1.71	2.96 2.64 2.35 2.07 1.57	2.72 2.40 2.09 1.79 1.00

摘自 Beyer WH: Handbook of Tables for Probability and Statistics,second edition,p 307,CRC Press,Inc.,1979

表2 F分布的分位数表(F界值表)
(方差分析用，上行： P=0.05 下行： P=0.01)

v2(较小 均方的自 由 度)	v1（较大均方的自由度）
	1	2	3	4	5	6	7	8	12	24	∞
1	161.4 4052	199.5 4999.5	215.7 5403	224.6 5625	230.2 5764	234.0 5859	236.8 5928	238.9 5982	243.9 6106	249.1 6235	254.3 6366
2	18.51 98.50	19.00 99.00	19.16 99.17	19.25 99.25	19.30 99.30	19.33 99.33	19.35 99.36	19.37 99.37	19.41 99.42	19.45 99.46	19.50 99.50
3	10.13 34.12	9.55 30.82	9.28 29.46	9.12 28.71	9.01 28.24	8.94 27.91	8.89 27.67	8.85 27.49	8.74 27.05	8.64 26.60	8.53 26.13
4	7.71 21.20	6.94 18.00	6.59 16.69	6.39 15.98	6.26 15.52	6.16 15.21	6.09 14.98	6.04 14.80	5.91 14.37	5.77 13.93	5.63 13.46
5	6.61 16.26	5.79 13.27	5.41 12.06	5.19 11.39	5.05 10.97	4.95 10.67	4.88 10.46	4.82 10.29	4.68 9.89	4.53 9.47	4.36 9.02
6	5.99 13.75	5.14 10.92	4.76 9.78	4.53 9.15	4.39 8.75	4.28 8.47	4.21 8.26	4.15 8.10	4.00 7.72	3.84 7.31	3.67 6.88
7	5.59 12.25	4.74 9.55	4.35 8.45	4.12 7.85	3.97 7.46	3.87 7.19	3.79 6.99	3.73 6.84	3.57 6.47	3.41 6.07	3.23 5.65
8	5.32 11.26	4.46 8.65	4.07 7.59	3.84 7.01	3.69 6.63	3.58 6.37	3.50 6.18	3.44 6.03	3.28 5.67	3.12 5.28	2.93 4.86
9	5.12 10.56	4.26 8.02	3.86 6.99	3.63 6.42	3.48 6.06	3.37 5.80	3.29 5.61	3.23 5.47	3.07 5.11	2.90 4.73	2.71 4.31
10	4.96 10.04	4.10 7.56	3.71 6.55	3.48 5.99	3.33 5.64	3.22 5.39	3.14 5.20	3.07 5.06	2.91 4.71	2.74 4.33	2.54 3.91
12	4.75 9.33	3.89 6.93	3.49 5.95	3.26 5.41	3.11 5.06	3.00 4.82	2.91 4.64	2.85 4.50	2.69 4.16	2.51 3.78	2.30 3.36
14	4.60 8.86	3.74 6.51	3.34 5.56	3.11 5.04	2.96 4.69	2.85 4.46	2.76 4.28	2.70 4.14	2.53 3.80	2.35 3.43	2.13 3.00
16	4.49 8.53	3.63 6.23	3.24 5.29	3.01 4.77	2.85 4.44	2.74 4.20	2.66 4.03	2.59 3.89	2.42 3.55	2.24 3.18	2.01 2.75
18	4.41 8.29	3.55 6.01	3.16 5.09	2.93 4.58	2.77 4.25	2.66 4.01	2.58 3.84	2.51 3.71	2.34 3.37	2.15 3.00	1.92 2.57
20	4.35 8.10	3.49 5.85	3.10 4.94	2.87 4.43	2.71 4.10	2.60 3.87	2.51 3.70	2.45 3.56	2.28 3.23	2.08 2.86	1.84 2.42
30	4.17 7.56	3.32 5.39	2.92 4.51	2.69 4.02	2.53 3.70	2.42 3.47	2.33 3.30	2.27 3.17	2.09 2.84	1.89 2.47	1.62 2.01
40	4.08 7.31	3.23 5.18	2.84 4.31	2.61 3.83	2.45 3.51	2.34 3.29	2.25 3.12	2.18 2.99	2.00 2.66	1.79 2.29	1.51 1.80
60	4.00 7.08	3.15 4.98	2.76 4.13	2.53 3.65	2.37 3.34	2.25 3.12	2.17 2.95	2.10 2.82	1.92 2.50	1.70 2.12	1.39 1.60
120	3.92 6.85	3.07 4.79	2.68 3.95	2.45 3.48	2.29 3.17	2.17 2.96	2.09 2.79	2.02 2.66	1.83 2.34	1.61 1.95	1.25 1.38
∞	3.84 6.63	3.00 4.61	2.60 3.78	2.37 3.32	2.21 3.02	2.10 2.80	2.01 2.64	1.94 2.51	1.75 2.18	1.52 1.79	1.00 1.00

摘自 Beyer WH: Handbook of Tables for Probability and Statistics,second edition,p 306,308,CRC Press,Inc.,1979
F分布与其他分布的关系：
(1) 当v1 =1时，F分布与t分布的分位数有如下关系：
单侧Fα(1,v)=双侧tα,ν2,(4)
例如，F₀.₀₅(₁₁₀)=4.96=(2.228)²＝t20.₀₅₁₀。
(2)当ν₂为无穷大时，F分布与x²分布的分位数有如下关系：
Fα(ν,∞)=xα,ν2/ν,(5)
例如，F_0.05(8,∞)＝1.94=15.51/8=x²_0.05,8/8。
(3) R. A. Fisher提出了样本方差之比的z分布，并制成了不同ν1、ν2时的z界值表。其后G. W. Snede-的关系式将其化成F值，以方便应用。为了尊重Fisher，故以其第一字母F来命名两样本方差之比的统计量。
用途
(1)方差齐性检验。即检验两样本所来自的两正态总体的方差是否相等，这时F等于两样本方差之比。
(2)方差分析。在方差分析中，F等于两个均方之比。
F检验时资料的适用条件是： 样本取自正态总体。作多个样本均数比较时，要求各正态总体的方差相等(经方差齐性检验，方差为齐性)。

F分布F distribution

样本统计量F = nx²₁/mx²₂ (m为分子自由度，n为分母自由度)的分布。密度函数为

式中Г为加玛函数，由美国统计学家斯纳德克(G.W.Snedecor)提出。分布曲线的形状随自由度m,n而异。当m,n增大时，分布曲线近于对称。若m,n极大，则趋于正态。F分布可用于方差齐性检验，也可用于方差分析的统计方法中。有根据F密度函数编制的F表供应用。

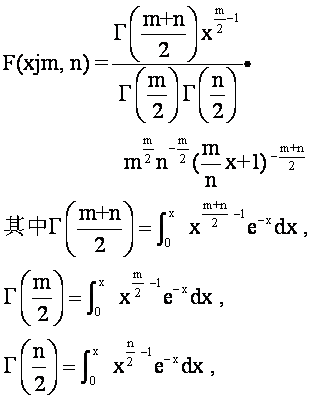
F分布Fdistribution

一种重要的小子样分布。为美国统计学家斯纳德柯(Snedecor,G.W.)所推导而得。其主要作用是检验方差的同一性。F分布的图像为单峰的偏态曲线，当其自由度m固定时，另一自由度n愈大则曲线愈接近对称，n愈小则右尾愈长。它的数学期望=n/n-2, (n>2)；方差=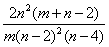(n>4)。两个独立N (0,1)的样本估计方差的比值：
i=1服从F(m,n)F分布经常用于方差分析，回归分析，两正态总体方差对比检验，二项分布的统计估计和统计检验等。因此，它是统计中的重要分布之一。

F分布F-distribution

抽样分布的一种。由英国统计学家费希尔(Ronald A. Fisher, 1890—1962)和斯奈蒂考(George Waddel Snedecor, 1881—1974)于20世纪20年代提出。若随机变量ξ服从χ²〖KG-*4〗(m)分布，m为自由度，η服从自由度为n的χ²〖KG-*4〗(n)分布，则随机变量F=(χ²〖KG-*4〗(m)/m)/(χ²〖KG-*4〗(n)/n)服从F分布。其密度函数曲线如下图，图中F(1, 5)、F(10, 10)、F(5, 4)表示分子、分母自由度依次为m=1、 n=5, m=10、 n=10, m=5、 n=4时F分布函数曲线。当m、n趋于无穷大时，F分布趋近于正态分布。心理学研究中如果从同一正态总体中随机抽取容量为n₁及n₂的两个样本，其样本方差比率分布服从F分布，由此可分析任意两个样本方差是否取自同一总体。

F分布

样本统计量概率分布的一种。由英国数理统计学家费希尔(R.A.Fisher)和斯奈蒂考(G.W.Snedecor)20世纪20年代提出。若随机变量ξ服从χ²_(m)分布，m为自由度，η服从自由度为n的χ ²_(n)分布，则随机变量F=(χ ²_(m)/m)/(χ ²_(n)/n)服从F分布。