随机变量的数学期望
数学期望就是随机变量的按照概率规律求出的加权平均值.
一维随机变量的数学期望E(X)
1.离散型随机变量
①有限型:若X的分布律为P{X=xi}=pi,i=1,2,…,n,则X的数学期望为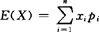 .
.
②无限型:P{X=xi}=pi,i=1,2,…,
如果级数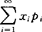 绝对收敛,则X的数学期望为
绝对收敛,则X的数学期望为
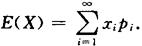
2.连续型随机变量
设X的密度函数为f(x),如果广义积分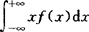 绝对收敛,则X的数学期望为
绝对收敛,则X的数学期望为
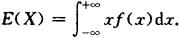
二维随机变量的数学期望
1.离散型随机变量
设(X,Y)的联合分布律为P{X=xi,Y=yi}=pij.两个边缘分布律分别为
P{X=xi}=pi.,P{Y=yi}=p.j,
则X,Y的数学期望分别为
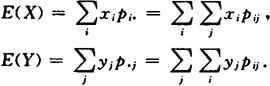
2.连续型随机变量
设(X,Y)的联合密度函数为f(x,y),边缘密度函数分别为fX(x),fY(y),则X,Y的数学期望分别为
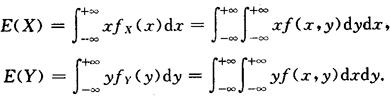
函数的数学期望
1.一维随机变量
若Y=g(X),E(Y)=E[g(X)].
(1)离散型随机变量
设X的分布律为P{X=xi}=pi,则Y的数学期望为
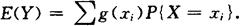
(2)连续型随机变量
设X的概率密度函数为f(x),则Y的数学期望为
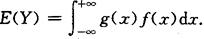
2.二维随机变量
若Z=g(X,Y),E(Z)=E[g(X,Y)].
(1)离散型随机变量
设(X,Y)的联合分布律为P{X=xi,Y=yi}=pij,则Z的数学期望为
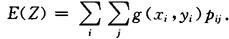
(2)连续型随机变量
设(X,Y)的联合密度函数为f(x,y),则Z的数学期望为
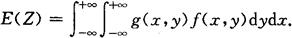
数学期望的性质(假设期望存在)
(1)若C为常数,则E(C)=C.
(2)若a为常数,则E(aX)=aE(X).
(3)E(X±Y)=E(X)±E(Y).
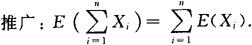
(4)若X,Y独立,则E(XY)=E(X)E(Y).
推广:若X1,X2,…,Xn相互独立,则
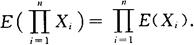
- 禅真逸史是什么意思
- 禅祖是什么意思
- 禅祚是什么意思
- 禅窟是什么意思
- 禅絮沾泥是什么意思
- 禅经是什么意思
- 禅者是什么意思
- 禅者王福省号觉庵。余不知禅,何以应福省?聊据己见塞白,然乎?否哉太虚!老僧千眼观音当一照我是什么意思
- 禅臣洋行是什么意思
- 禅舍是什么意思
- 禅舫为顺上人赋是什么意思
- 禅衣是什么意思
- 禅衲是什么意思
- 禅袍是什么意思
- 禅襦是什么意思
- 禅观是什么意思
- 禅观法是什么意思
- 禅让是什么意思
- 禅让制是什么意思
- 禅让制到世袭制是什么意思
- 禅让和接替是什么意思
- 禅诏是什么意思
- 禅话是什么意思
- 禅语是什么意思
- 禅谕是什么意思
- 禅趣是什么意思
- 禅道虚空 先贤神髓入真行是什么意思
- 禅那是什么意思
- 禅里是什么意思
- 禅野叟是什么意思
- 禅钖是什么意思
- 禅镇是什么意思
- 禅门是什么意思
- 禅门口诀是什么意思
- 禅门太极拳是什么意思
- 禅门日诵是什么意思
- 禅门章是什么意思
- 禅门至六祖,衣钵无人得。是什么意思
- 禅门要略是什么意思
- 禅阁是什么意思
- 禅院是什么意思
- 禅陵是什么意思
- 禅隐山人是什么意思
- 禅静是什么意思
- 禅鞋是什么意思
- 禅龛是什么意思
- 禅(泛指一切佛教事物)是什么意思
- 禆是什么意思
- 禆正是什么意思
- 禆补匡正是什么意思
- 禇是什么意思
- 禈是什么意思
- 禈中是什么意思
- 禉是什么意思
- 禊是什么意思
- 禊事是什么意思
- 禊事活动之日是什么意思
- 禊亭是什么意思
- 禊兰堂是什么意思
- 禊宴是什么意思