线性相关分析
对于二元连续型(1)总体(X,Y)T,人们研究其两个分量之间的关系,途径之一是采用(随机)自变量X的如下线性函数作为(随机)因变量Y的模拟:
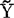 =β0+βX (48.3.1)
=β0+βX (48.3.1)
线性模拟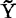 ,在每一个观测单元上的取值,即总体Y的线性模拟值
,在每一个观测单元上的取值,即总体Y的线性模拟值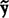 ,与总体X在同一个观测单元上的取值X之间具有与(48.3.1)式同样的线性关系:
,与总体X在同一个观测单元上的取值X之间具有与(48.3.1)式同样的线性关系:
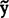 x=β0+βx (48.3.1)1
x=β0+βx (48.3.1)1
x—y平面上用(48.3.1)1式表示的直线称为总体Y关于总体X的一元回归直线。
为了由总体( )的样本观测值(
)的样本观测值(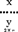 )=(
)=(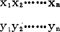 )用最小二乘法求得截距β0和斜率β的估计值b0和b,从而求得线性模拟
)用最小二乘法求得截距β0和斜率β的估计值b0和b,从而求得线性模拟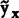 的估计值
的估计值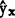 =b0+bx,需要首先定义样本观测值
=b0+bx,需要首先定义样本观测值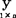 与
与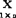 的相关矩lyx,协方差Syx和相关系数r:
的相关矩lyx,协方差Syx和相关系数r:
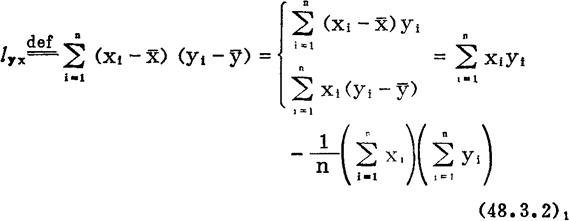
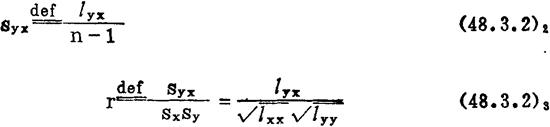
最小二乘法是求得满足下式的b0和b的方法(2):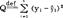 =min,其中:对i=1—n(48.3.3)
=min,其中:对i=1—n(48.3.3)
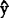 i=b0+bx1,是线性模拟
i=b0+bx1,是线性模拟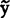 i=β0+βxi的估计值
i=β0+βxi的估计值
首先由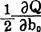 =0推出b0=
=0推出b0=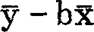 ,将其代入1=0,解出
,将其代入1=0,解出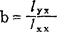 。下列简单的推导表明,这样求得Q的驻点是Q的最小值点:
。下列简单的推导表明,这样求得Q的驻点是Q的最小值点:
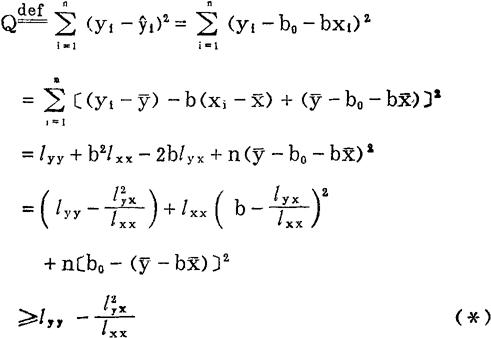
以上推导过程最后一步“≥”的等号当且仅当用求得的驻点
(b0,b)=(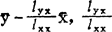 )代入Q(b0,b)时成立。可以把(*)式最左端与最后一个等式右端改写如下:令
)代入Q(b0,b)时成立。可以把(*)式最左端与最后一个等式右端改写如下:令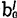 =b0+
=b0+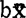
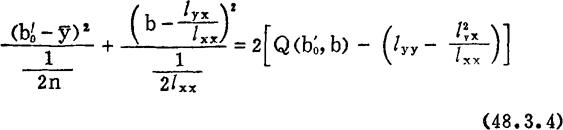
上式表明,Q=Q(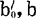 )在
)在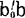 -Q空间的图形是以(
-Q空间的图形是以(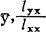 ,lyy-
,lyy-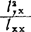 )为顶点,开口向上的椭圆抛物面,其顶点是最低点,即Q的最小值点,如图48—1所示。
)为顶点,开口向上的椭圆抛物面,其顶点是最低点,即Q的最小值点,如图48—1所示。
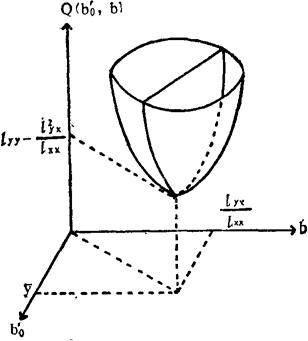
图48—1
这样,就得到了(48.3.1)1式的最小二乘估计:
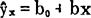 ,其中:
,其中: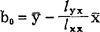
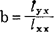 (48.3.1)2直线(48.3.1)2式通过点(
(48.3.1)2直线(48.3.1)2式通过点(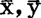 )。又由(*)式可知:minQ=lyy-
)。又由(*)式可知:minQ=lyy-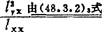 lyy(1-r2) (48.3.5)由上式可知相关系数具有如下性质(3):
lyy(1-r2) (48.3.5)由上式可知相关系数具有如下性质(3):
(1)|r|≤1,这是因为minQ≥0。
(2)如果r=±1,则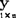 与
与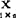 完全线性相关:
完全线性相关:
由于minQ=Q(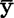 ±
±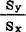 X,±
X,±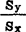 )=0,所以对i=1—n,y1=
)=0,所以对i=1—n,y1=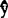 1=
1=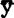 ±
±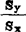 (xi-X),n个点(xi,yi),i=1—n完全位于回归直线上。
(xi-X),n个点(xi,yi),i=1—n完全位于回归直线上。
(3)如果r=0,则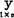 与
与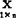 线性无关:
线性无关:
由于minQ=Q(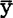 ,0)=lyy,所以对i=1—n,
,0)=lyy,所以对i=1—n,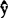 i≡
i≡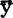 ,不随xi改变。回归直线
,不随xi改变。回归直线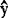 x=
x=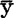 不能表达
不能表达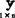 与
与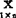 之间或者存在某种非线性关系或者没有关系。
之间或者存在某种非线性关系或者没有关系。
(4)|r|越大,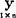 与
与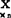 线性相关越密切:
线性相关越密切:
minQ越小,表示n个点(xi,y1),i=1-—n越接近回归直线。
(5)r>0称为正相关;r<0称为负相关:
b>0,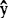 i随xi增大而增大,表示yi随xi增大有增大的趋势;b<0,
i随xi增大而增大,表示yi随xi增大有增大的趋势;b<0,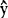 i随xi增大而减小,表示yi随xi增大有减小的趋势。
i随xi增大而减小,表示yi随xi增大有减小的趋势。
样本观测值的相关系数r表示样本观测值]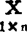 线性相关的密切程度以及正、负相关,这跟总体相关系数ρ对于总体Y与X所表示的概念是一样的。推断ρ
线性相关的密切程度以及正、负相关,这跟总体相关系数ρ对于总体Y与X所表示的概念是一样的。推断ρ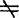 0并且用r作为它的估计值,是以|r|>rα(n-2)为前提。只有在这种情形,(48.3.1)1式中的斜率
0并且用r作为它的估计值,是以|r|>rα(n-2)为前提。只有在这种情形,(48.3.1)1式中的斜率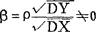 ,才有必要用(48.3.1)2式作为β0、β以及(48.3.1)1式的最小二乘估计。rα(n-2)可以查“检验相关系数ρ=0的临界值(rα)表”得到,n-2是自由度。相关分析的步骤如表48—1所示。
,才有必要用(48.3.1)2式作为β0、β以及(48.3.1)1式的最小二乘估计。rα(n-2)可以查“检验相关系数ρ=0的临界值(rα)表”得到,n-2是自由度。相关分析的步骤如表48—1所示。
表48—1
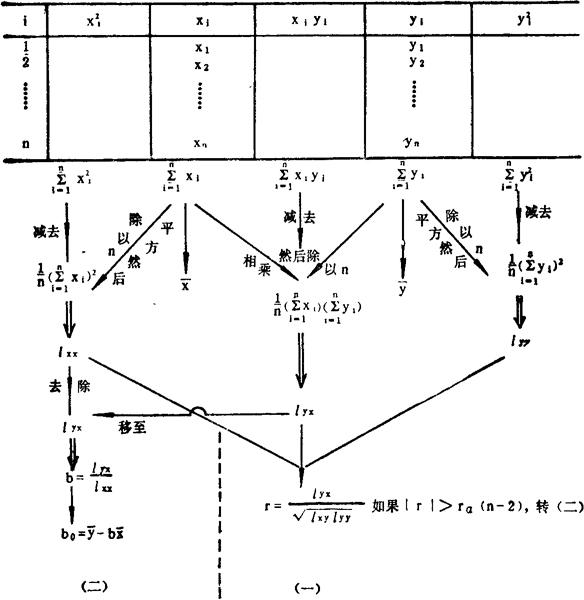
可以使用SHARP-5002计算器的如下程序求得r与b0、b以及ρ的置信度为1—α的置信区间:
(1)—→STAT
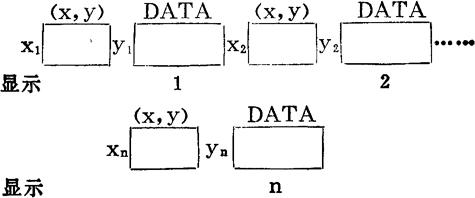
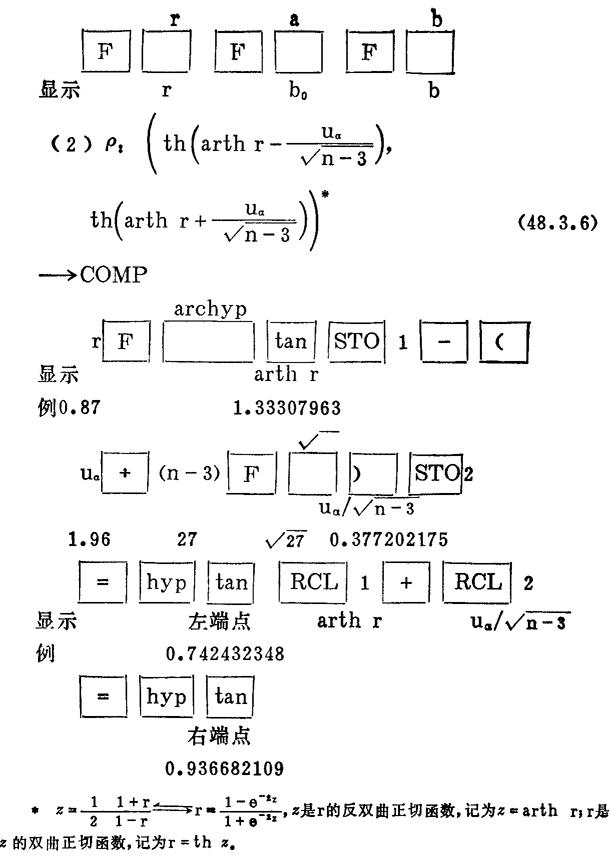
在上例中,r=0.87,u5%=1.96,n=30,算得ρ的95%置信区间是(0.7424,0.9367)。置信度1-α表示可靠性。uα可以查“标准正态分布的双侧分位数(uα)表”得到,一般常用u5%=1.96。
对于三元连续型总体(X1,X2,Y)T,如果研究工作需要以X1和X2为(随机)自变量,而以Y为(随机)因变量,则类似于(48.3.1)式和(48.3.1)1式,有:
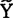 =β0+β1X1+β2X2 (48.3.7)
=β0+β1X1+β2X2 (48.3.7)
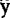 x=β0+β1x1+β2x2 (48.3.7)1
x=β0+β1x1+β2x2 (48.3.7)1
x1x2-y立体空间中的平面(48.3.7)1式称为总体Y关于总体X1、X2的二元回归平面。它的最小二乘估计是:
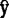 x=b0+b1X1+b2X2,其中:b0=
x=b0+b1X1+b2X2,其中:b0=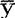 -b1
-b1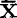 1—b2X2(48.3.7)2
1—b2X2(48.3.7)2
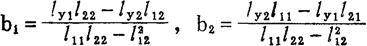
以上求b1和b2的公式右端各量的足码1与2分别是总体X1的取值x1与总体X2的取值x2的代号。这里假设行列式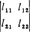 =l11l22-l
=l11l22-l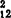 >0。计算
>0。计算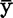 ,
,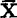 1,
1,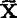 2;l11,l12=l21,l22;ly1,ly2是使用总体
2;l11,l12=l21,l22;ly1,ly2是使用总体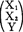 的样本观测值
的样本观测值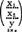 =
=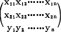 。
。
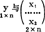 线性相关的密切程度用下列复相关系数表示:
线性相关的密切程度用下列复相关系数表示:
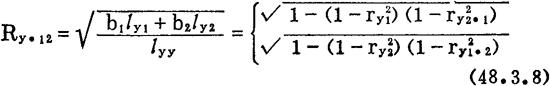
上式中的b1和b2是β1和β2的最小二乘估计值,由(48.3.7)2式求出。ry1.2和ry2.1称为偏相关系数:ry1.2从ry1中消除了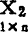 的影响;ry2.1从ry2中消除了
的影响;ry2.1从ry2中消除了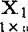 的影响。上述的“影响”来自
的影响。上述的“影响”来自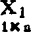 与
与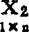 的(线性)相关系数r12。
的(线性)相关系数r12。
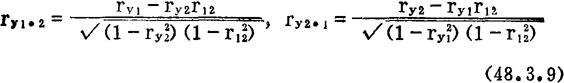
(编者:刘长安 审者:孙尽善)
- 二审是什么意思
- 二审刑事裁定书是什么意思
- 二审判决是什么意思
- 二审判决、裁定是什么意思
- 二 审判工作概况是什么意思
- 二审合议庭是什么意思
- 二审合议庭的组成是什么意思
- 二审审理方式是什么意思
- 二审密是什么意思
- 二审抗诉的理由是什么意思
- 二审期限是什么意思
- 二审案件的处理是什么意思
- 二审民事裁定书是什么意思
- 二审程序是什么意思
- 二审程序参照一审程序进行是什么意思
- 二审裁定是什么意思
- 二 审计制度是什么意思
- 二宣丸是什么意思
- 二宣汤是什么意思
- 二室凌青天,三花含紫烟。是什么意思
- 二室模型是什么意思
- 二宫白梨是什么意思
- 二家咏古诗是什么意思
- 二家子是什么意思
- 二家宫词是什么意思
- 二 家庭结构和功能的变迁是什么意思
- 二家旁人是什么意思
- 二家梁是什么意思
- 二家罗是什么意思
- 二家词钞是什么意思
- 二家诗抄是什么意思
- 二家诗选是什么意思
- 二家诗钞是什么意思
- 二寰是什么意思
- 二寸藤冠狂道士,一编蠹简老书生。是什么意思
- 二对是什么意思
- 二 对外承包工程和劳务合作是什么意思
- (二)对资产阶级史学的批判是什么意思
- 二 寿县是什么意思
- 二将争功是什么意思
- 二将城是什么意思
- 二将城遗址是什么意思
- 二尊是什么意思
- [二]尊祖祭是什么意思
- 二小儿是什么意思
- 二小子不拉纤是什么意思
- 二小的故事是什么意思
- 二小穿军装——规规矩矩是什么意思
- 二尕娃是什么意思
- 二尖是什么意思
- 二尖子是什么意思
- 二尖瓣是什么意思
- 二尖瓣中度狭窄是什么意思
- 二尖瓣临界性狭窄是什么意思
- 二尖瓣乳头肌功能失调是什么意思
- 二尖瓣交界分离术是什么意思
- 二尖瓣关闭不全是什么意思
- 二尖瓣前叶扑动是什么意思
- 二尖瓣前叶曲线是什么意思
- 二尖瓣前叶活动最大幅度是什么意思