Chebyshev集的太阳性和凸性

---

设E为赋范线性空间，M为E中子集，令，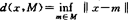

PMt=｛m；m∈M，‖x－m‖=d(x，M)｝

若对任何x∈E，PMx≠Φ，则称M为存在性集，如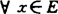，P_Mx为单点集，则称M为Chebyshev集。

为讨论最佳逼近的唯一性，Efimov和stechkin在1958年引入太阳集的概念：若由m∈P_Mx可推得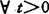有m∈P_Mxt，其中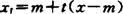，则称M为太阳集。

为了讨论Chebyshev集和太阳集、凸集间的关系，还需知下述概念：

M为有界紧集：M与E中任何球的交集是紧集。

M为逼近紧集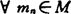：满足‖x－m_n‖→d(x，M)时，必有子列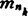收敛。

E为光滑空间：f∈E^*满足‖f‖=1f(x)=‖x‖称为x点的支撑泛函。

如果对每一x∈E，支撑泛函唯一，称E为光滑空间。

E为一致凸空间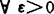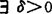：，，由‖x‖=‖y‖=1及‖x+y‖＞2－δ可推得‖x－y‖＜ε。

Chebyshev集、太阳集、凸集三者间的关系：(1)Banach空间E中有界紧Chebyshev集必为太阳集。(2)光滑空间E中存在性太阳集必凸。(3)一致凸空间E中逼近紧Chebyshev集必为太阳集。(4)实C(x)中逼近紧Chebyshev集是太阳集。

Dunham于1975年在C［0，1］中举出Chebyshev集不是太阳集的例，说明(4)中逼近紧不能省。

例：设ψ，R₊→R 严格单调并满足

ψ(0)=1，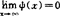

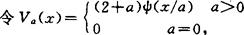
则M=｛V_a，a≥0｝是C［0，1］中Chebyshev集，但不是太阳集。

对Hillert空间H，由(2)(3)有：逼近紧Chebyshev集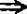存在性太阳集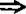凸集。去除逼近紧条件，在Hillert空间H中，Chebyshev集是否一定是凸集?这是至今未解决的问题。

当H不完备时，Johnson于1987年给出上述问题的否定解答，在内积空间中给出不凸的Chebyshev集

例：E=｛(x₁，x₂…x_n…)；x_n∈R，｛i；x_i≠0｝；x_i≠0｝为有限集｝。

令，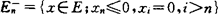

1=A₀＞A₁＞A₂＞…＞0，L₀=F₀=1

归纳地定义：

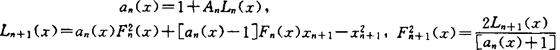
命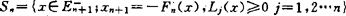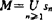，，则M为E中不凸的Chebyshev集。

讨论最佳远达问题，令

，

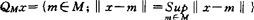即Q_Mx为M对x最远点全体。

如对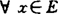，Q_Mx均为单点集，则称M为唯一远达集。

对赋范线性空间E，可讨论关于∑=｛x；‖x－c‖=r｝的反演变换

f(x)=c+(r²／‖x－c‖²)(x－c)

易见

f：E＼｛c｝→E＼｛c｝

当E为内积空间时，Klee指出：当S是E中不通过c的球面时，f(s)也是球面。利用上述反演变换，Klee证得下列论断有(2)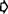(1)：(1)E中任何Chebyshev集是凸集；(2)E中任何唯一远达集是单点集。

虽然对许多具体空间，证实了唯一远达集的单点性，但对Hillert空间，这仍是一个悬而未决的问题。

对Hillert空间H的有界子集M，数

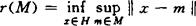
称为M的Chebyshev半径。满足

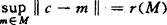
的c∈H称为M的Chebyshev中心。对Hillert空间的有界子集，Chebyshev中心存在且唯一。

Astaneh于1983年证得下述结果：

M是Hillert空间H中唯一远达集，c、r(M)为M的Chebyshev中心和Chebyshev半径，则M或为单点集，或对x∈(c，q(c))有

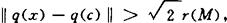
其中q(x)为远达点映照。

最后，介绍关于几乎Chebyshev集的一些结果：Stechkin于1963年对赋范线性空间E中子集M，引进唯一性集T_M=｛x；P_Mx为单点集，x∈ E｝。

如果E＼T_M至多是第1纲集，则称M为几乎Chebyshev集。并且证明'

一致凸空间中任何闭集都是几乎Chebyshev集。

1978年K．S．Lau将Stechkin的结果推进到自反、局一致凸空间。这里局一致凸的意义为：

记s=｛x；x∈E，‖x‖=1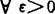｝，及x∈S，，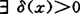

当y∈s，‖x+y‖＞2－δ(x)有‖x－y‖＜ε。

K．S．Lau同时举例说明：条件自反不可省，局一致凸不能减弱为严格凸。

1990年李冲将K．S．Lau的结果推广到K局一致凸空间，证得

自反的K局一致凸空间的任何闭子集是几乎k－Chebyshev集。

K局一致凸是指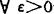：，x∈S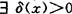，对任何x₁，x₂…x_k∈s及‖x+x₁+…x_k‖＞k+1－δ(x)有Sup

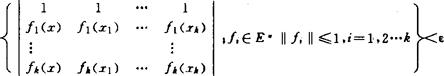
K几乎Chebyshev集意义是：对P_Mx定义维数 dimP_Mx=dim［Span(P_Mx－P_Mx)］，记

BM=｛x∈E；P_Mx≠Φ且dimP_Mx＜k｝

若E＼B_M至多是第一纲集，则称M是k－几乎Chebyshev集。

不同空间中Chebyshev集特性的研究已有不同程度的展开，随著进一步研究，期望会得到更全面更深入的结果。特别对Hillert空间中Chebyshev集是否是凸集的遗留问题可望得到解决。

从单目标逼近到多目标逼近，最佳共同逼近中相应的唯一性集的研究现已初步展开，近期可望得到更多更好的结果。

对非线性优化问题，甚至非线性多目标优化问题，对应于某种意义下最优解的唯一性问题也是值得研究的重要课题。

。【参考文献】：

1 EfimovN V.StechkinSB. DANSSSR, 1958,118:17～19

2 Efimov.N V.StechkinSB. D A N SSSR, 1959,127:254～ 257

3 KleeV. Math Annalen ,1961,142:292～304

4 Stechkin S B. Rev Roumaine Math Pur Appl, 1963,8:5～ 18

5 VlasovLP. MathZametki, 1967,2:191 ～ 200

6 Dunham C B. Math Bull, 1975,18:35～38

7 L'au K S. Indian University Math J, 1978,27:791～795

8 Astaneh A A. Indian J Pure Appl Math ,1983,14,(10): 1311～1317

9 JohnsonGG. J AT, 1987,51:289～332

10 李冲．几乎k－Chebyshev子集，1990，33(2)∶251～258

(浙江师范大学徐士英教授撰)

上一篇：Chebyshev中心
下一篇：现代科技综述大辞典上目录

"Chebyshev中心Chebyshev中心

---

设E是赋范线性空间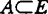，是有界子集，定义：

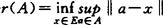
则称r(A)为A的Chebyshev半径，而A的Chebyshe中心就是。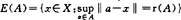

提出这一问题是很自然的。例如，由于试验误差，当我们不能确切地知道函数时，可以把它理解为一个集合，然后用单个的最优元素代表这个集合。

另外，Chebyshev中心在最优回复理论的研究中也有重要意义。

Chebyshev中心这一概念首先是Garkavi在1962年提出并研究的，并在1964年给出下面的结果：

定理G Banach空间E中每一有界集A至少有一Chebyshev中心y₀∈COA，当且仅当E是完备内积空间或E的维数2。

下面结果最早是由Kadets和Zamyatin在1968年对S=［a，b］给出的，一般情形是由Franchetti和Cheney给出的。

定理K－Z：B(S)(C(S)中任一有界集恒有非空的Chebyshev中心，其中S是任一拓扑空间，B(S)(C(S))是全体实有界(连续)函数所组成，并赋于一致范数。

对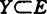，A的相对或限制(Chebyshev中心)，是

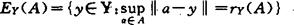
其中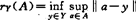，，为A的相对或限制Chebyshev半径。这一问题自60年代就有许多研究。

关于唯一性，1980年Amir和Ziegler定义了E关于子空间Y的严格凸性和各向一致凸性。

定理A－Z 设Y是E的子空间，则：(1)对任何紧子集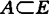，E_Y(A) 至多只有一个元当且仅当E关于Y是严格凸；(2)对任何有界集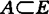，E_Y(A) 至多只有一个元当且仅当E关于Y是各向一致凸的。

关于相对Chebyshev中心的特征，当A是局部紧时，由于可转化成C(A、E)中的单元逼近，故可以毫无困难地得Kolmogorov型特征定理。但对一般的有界集A，要给出其Kolmogorov型特征定理并非易事。

1982年，Freilich和McLaughlin在Y是凸集时给出下列的Kolmogorov型特征。

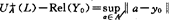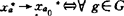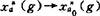定理F－M y₀∈E_y(A)当且仅当对任何y∈Y存在L∈extK满足且ReL(y－y₀)≤0，其中的闭单位球B^*。在K上赋以σ(K、G)拓扑：，，且K满足：(1)K是σ(K、G)紧。(2)任何a∈A，y∈Y，有。

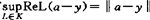而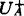(L)定义为：

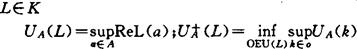
其中U(L)为在K上的开例域全体。

但定理F－M中的必要性未必成立，我们在1987年举例说明不真，并刻划了非线性情形下的相对Chebyshev中心的特征。

定理X－L 设Y是E中一子集，则下述论断等价：(1)对任何有界集F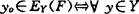，，存在L∈Y，使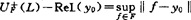且ReL(y－y₀)≤0；(2)Y是同时太阳集。即对任何有界集F，若y₀∈E_Y(F)，则y₀∈E_Y(F_a)，其中F_a=y₀+a(F－y₀)，a≥0。

关于Er(A)的非空性，即相对Chebyshev中心的存在性。若有某种紧性，例如局部有界紧或局部有界弱紧，且Y是闭或弱闭，则对任何有界集A，EY(A)非空。但是当Y没有任何紧性，则其研究相当困难。1991年，D．V．Pai和P．T．Nowrojij在E中的子空间Y引进R₁性质，这是单元逼近中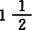一球性质的推广，并证明了下面的存在性定理。

定理P－N 设E是Banach空间，Y是E的子空间，若Y关于E中所有的有界集(紧集)有R₁性质，则对任何有界集(紧集)A，E_Y(A)≠Φ。

目前有众多的文献在研究EY(A)的连续性与强唯一性，对E中任何两个有界集A、B，其Hausdorff距离定义为：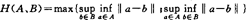

1982年，P．Szeptycki和F．S．Var VLeck证明了下述定理。

定理S－V 若E是Hilbert空间，则对任何两个紧子集A、B有

‖ E(A)－E(B)‖²≤［r(A)+r(B)+H(A，B)］H(A，b)(*)

并提出下述两个问题

问题S－V－I：若A、B没有紧性(*)式是否成立?

问题S－V－I：当E是一致凸空间时，‖E(A)－E(B)‖是否有类似于(*)式的估计?

1988年，我们给问题S－V－I一个肯定回答；

定理L：设E是Hilbert空间，Y是E中凸集，则对任何有界集A，B有

‖E_r(A)－E_r(B)‖²≤［rY(A)+rY(B)+H(A，B)］H(A，B)

问题S－V－Ⅱ，在1989年由王嘉平与俞鑫泰解决。

在当前及今后的研究中，相对Chebyshev中心的定量分析，如相对Chebyshev中的实现，相对Chebyshev半径的计算等，将成为热点和趋势。

。【参考文献】：

1 Garkavi A L, The Chebyshev centers and the convex hull of a set,Uspehi Mat Nauk,1964,19:139-145

2 Amir D , Ziegler Z. Relative Chebyshev Centers in Normed Linear Space I,J Approx Theory, 1980,29:235-252

3 Franchetti C , Cheney E W. Simultaneous approximation and restricted Chebyshev centers in fanction spaqes, in "" Approximation Theory andd Applications"", ed. by Z Ziegler,Academic Press, New. York, 1981, 65～88

4 Freilich J H , Mclaughlin H W. Approximation of bounded sets,JApprox Theory,1982,34:145～158

5 Franchetti C , Cheney E W.The embedding of Proximinal sets J Approx Theory, 1986,48:213～225

6 徐士英，李冲，等．最佳同时逼近的特征．数学学报，1987，30(4)∶528～535

7 Szeptycki P , Van Vleck F S: Centers and nearest points of sets,Proc A,M,S,85 1987,8S:27～31

8 Li Chong. On a problem on Chebyshev centers, Advance in Math,1988,17(2) ,216～217

9 Wang J P, Yu X T. Chebshev centers, Chebyshev centers and the Hausdorff metric,Manuscripta Math, 1989,63:115 ～128

(杭州商学院李冲副教授撰；徐士英审)

上一篇：Bers空间中之逼近
下一篇：现代科技综述大辞典上目录

"checkcheck

---

【词性】：v．

【释义】：

❶ 遏制，制止❷ 检查，核对

check asthma by eliminating phlegm消痰平喘

check exuberance of yang潜阳

check pain止痛

check the liver平肝

reinforce the earth to check the wood培土抑木

When pathogenic cold invades the superficial portion of the boby and the defensive yang energy is checked．寒邪袭表，卫阳被抑。